Department of Computer Science
CSU Stanislaus
California State University

MarieSimEx: The Marie Computer Simulator Extension

Xuejun Liang

June 2021

Introduction

MarieSimEx is an extension to MarieSim which is a computer architecture simulator based on the MARIE architecture and designed to teach beginning computer organization and architecture. Using MarieSim, a simple accumulator-based assembly language program can be assembled and run. Users can track the values of internal CPU registers and the memory contents in MarieSim environment as each instruction is executed. But, MarieSim is too simple and thus unable to support some important concepts in computer architecture such as immediate and indexed addressing modes, stack, and recursive subroutine. Meanwhile, MarieSim does not support of defining a label (symbol) to hold the address of another label (symbol) symbolically. Programmers have to compute (count) the address of a label manually and then hardcoded it into their code.

In order to solve these problems, an extension to MarieSim, called MarieSimEx, is developed. In MarieSimEx, a directive LAB is added for defining a label to hold the address of another label symbolically. An instruction LIMM is added for loading an immediate constant into the accumulator AC. This instruction is apparently an extension of MARIE instruction CLEAR which loads zero into AC. More importantly, a stack pointer is added to support subroutine linkage via stack. A stack frame can be built for a subroutine to hold the return address, input arguments, output results, local variables, etc. Therefore, the MARIE subroutine call instruction JNS is revised to put the return address on top of stack instead of the memory slot just before the first instruction of the subroutine. Finally, a new instruction JR is added for subroutine return.

In the following, the MARIE instruction set is described briefly along with the new extension. Then, two example applications are used for illustrating and comparing the differences between MarieSim and MarieSimEx. The first application is to compute the sum of an array of numbers and the second is to compute Fibonacci numbers. Different programming techniques are used to compute Fibonacci numbers so that students can have a better understanding of global variables, local variables, stack, subroutine, and recursion. Finally, two programming assignments are also provided for student practice.

MARIE Instruction Set and Extension

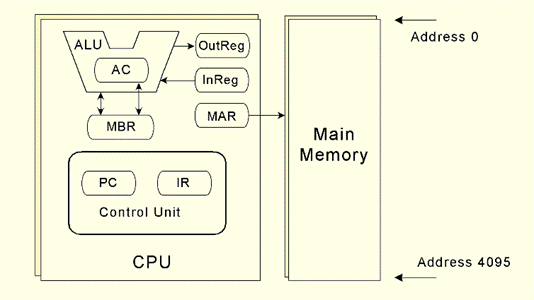
The MARIE architecture has the following characteristics:

· Binary, two's complement data representation.

· Stored program, fixed word length data and instructions.

· 4K words of word-addressable main memory.

· 16-bit data words.

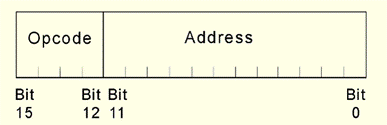
· 16-bit instructions, 4 for the opcode and 12 for the address.

· A 16-bit arithmetic logic unit (ALU).

· Seven registers for control and data movement.

The MARIE architecture is shown graphically as below.

The MARIE instruction encoding format is shown as below.

The MARIE instructions along with the new extension (in red color) are shown in the following table.

Opcode	Instruction	Meaning	Address mode
			MarieSim	MarieSimEx
0000	JnS X	Mem[X] ß PC & PC ß X+1	Direct
	JnS X	Push PC & PC ß X		Direct
0001	Load X	AC ß Mem[X]	Direct	Direct, Indexed
0010	Store X	Mem[X] ß AC	Direct	Direct, Indexed
0011	Add X	AC ß AC + Mem[X]	Direct	Direct, Indexed
0100	Subt X	AC ß AC – Mem[X]	Direct	Direct, Indexed
0101	Input	AC ß value from keyboard	N/A	N/A
0110	Output	Display value in AC on screen	N/A	N/A
0111	Halt	Terminate program	N/A	N/A
1000	Skipcond 000	Skip next instruction if AC < 0	N/A	N/A
	Skipcond 400	Skip next instruction if AC = 0	N/A	N/A
	Skipcond 800	Skip next instruction if AC > 0	N/A	N/A
1001	Jump X	PC ß X	Direct	Direct, Indexed
1010	Clear	AC ß 0	N/A
	Limm Imm	AC ß Imm		Immediate
1011	AddI X	AC ß AC + Mem[Mem[X]]	Indirect	(Indexed) Indirect
1100	JumpI X	PC ß Mem[X]	Indirect	(Indexed) Indirect
1101	LoadI X	AC ß Mem[Mem[X]]	Indirect	(Indexed) Indirect
1110	StoreI X	Mem[Mem[X]] ß AC	Indirect	(Indexed) Indirect
1111	JR	Pop PC		N/A

Note 1: X can be either a hexadecimal literal or a label (symbol) and is used as a memory address in MarieSim and Mem[X] represents the content at the memory location X.

Note 2: In MarieSimEx, Imm is a 12-bit decimal constant integer. When using direct addressing, X is the same as that in MarieSim. But when using stack-relative addressing, X has the format: $±Offset, where $ represents the stack pointer (the address of top of stack) which is stored in a reserved memory location SP and Offset is a 10-bit decimal constant integer. The two bits right before Offset inside an instruction are set to be 11. This indicates that stack-relative addressing is used. The memory address represented by $±Offset can be computed by Mem[SP]±Offset. Please note that using a reserved memory location to hold the stack pointer instead of using a dedicated register will have no impact on the original MARIE architecture including its micro architecture so that the user interface of MarieSim can be used for MarieSimEx with a minor modification. Both the value of stack pointer and the contents in stack can be observed from the memory monitor area of the MarieSim environment. If using a dedicated register, then the MARIE datapath has to be changed.

Note 3: The MARIE architecture has 4K words of word-addressable main memory. The stack grows towards higher memory address end and starting from 3072. Therefore, the stack occupies 1K out of 4K MARIE word-addressable memory space. A valid MARIE memory address is still in between 0 and 4095. It is possible that the user program code and/data will occupy (overwrite) the stack memory. So, when your program utilizes the stack, please make sure your program code and data are located in memory from address 0 to address 3070. The stack pointer is located at memory location 3071.

Note 4: Two important operations on stack are push and pop. Push X operation (or pseudo-instruction) will push memory content at memory address X, i.e. Mem[X], on top of stack and Pop X operation (or pseudo-instruction) will store the content on top of stack in memory location X and remove it from stack. These two pseudo-instructions can be implemented by (or equivalent with) sequences of assembly instructions, respectively, as shown in the following table.

Push X	Pop X
Limm 1 Add SP Store SP Load X StoreI SP	loadI SP Store X Limm -1 Add SP Store SP

Note 5: The pseudo-instructions Push X and Pop X will be used in the assembly language programs in this article for the sake of saving space. In order to assemble and to run your programs, you must expand Push X and Pop X, i.e., replace them with their corresponding sequences of instructions as shown above, respectively. Currently, MarieSimEx does not support pseudo-instructions such as Push X and Pop X.

MARIE Directives and Extension

Directives are instructions to assemblers. MarieSim has five directives. Directive ORG defines the starting address of the program. Directives DEC, OCT, and HEX define named constant in decimal, octadecimal, and hexadecimal, respectively. Directive END indicates the end of the program. MarieSimEx adds one more directive LAB which defines a named hexadecimal constant specified either by a hexadecimal literal or a label symbolically.

How to Install and Use MarieSim and MarieSimEx

Please reference the MarieSim quick guide for installing and using MarieSim. You can install and use MarieSimEx in the exactly same way as for MarieSim. The Simulator Jar Files (Executables) can be downloaded using the following links.

· MarieSim (marieSim.jar)

· MarieSimEx (marieSimEx.jar)

Assembly Language Program Examples Using MarieSim and MarieSimEx

Example 1: This example is to compute sum of an array of numbers. The code in the left of the following table is for MarieSim and MarieSimEx and the right for MareiSimEx only. It can be seen that the new instruction Limm and the new directive LAB are applied in the code for MarieSimEx. These two new extensions make programmers easier to deal with address manipulation and give programmers a greater ability to deal with immediate operands.

/ Code for MarieSim and MarieSimEx ORG 100 /Program starts from 0x100 Load Addr /Load address of first number to be added Store Next /Store this address is our Next pointer Load Num /Load the number of items to be added Subt One /Decrement Store Ctr /Store this value in Ctr to control looping Loop, Load Sum /Load the Sum into AC AddI Next /Add the value pointed to by location Next Store Sum /Store this sum Load Next /Load Next Add One /Increment by one to point to next address Store Next /Store in our pointer Next Load Ctr /Load the loop control variable Subt One /Subtract one from the loop control variable Store Ctr /Store this new value in loop control variable Skipcond 000 /If control variable < 0, skip next instruction Jump Loop /Otherwise, go to Loop Halt /Terminate program Addr, Hex 117 /Numbers to be summed start at location 117 Next, Hex 0 /A pointer to the next number to add Num, Dec 5 /The number of values to add Sum, Dec 0 /The sum Ctr, Hex 0 /The loop control variable One, Dec 1 /Used to increment and decrement by 1 Dat, Dec -10 /The values to be added together Dec 15 Dec -20 Dec 25 Dec 30

/ Code for MarieSimEx ORG 100 Load Addr Store Next Limm -1 Add Num Store Ctr Loop, Load Sum AddI Next Store Sum Limm 1 Add Next Store Next Limm -1 Add Ctr Store Ctr Skipcond 000 Jump Loop Halt Addr, Lab Dat Next, Hex 0 Num, Dec 5 Sum, Dec 0 Ctr, Hex 0 Dat, Dec -10 Dec 15 Dec -20 Dec 25 Dec 30

Example 2: Compute the Fibonacci number which is defined by

A C++ code that computes Fibonacci number using a loop is shown below. The algorithm used in this C++ code will be used (translated) in the assembly language programs later so that comparisons can be made. Note that variable A is used for Fib(N-2), B for Fib(N-1), C for Fib(N), and I for the loop control.

int main() { //compute Fib(N)

int I, A, B, C, N

std::cin >> N; //get input N, say 10.

if (N < 2)

C = N;

else {

A = 0; B = 1;

for (I = 2; I <= N; I++) {

C = B + A; A = B; B = C;

}

}

std::cout << C;

return 0;

}

Four methods will be used to compute Fibonacci numbers. The first is using a loop, the second using a function with global variables, the third using a function with local variables, and the fourth using a recursive function. The first two methods can be applied when using either MarieSim or MarieSimEx, while the last methods can be applied when using MarieSimEx only.

Method 1 (Using Loop): This is done by simply translating the above C++ code into MARIE assembly code directly. Five variables with the same names as in C++ are defined with initial values. The program gets input N first, then computes the Fibonacci number and saves into C, and finally prints the result C. Note that code for MarieSim has to define an extra variable One to hold a constant number 1, while the code for MarieSimEx can use the constant number 1 directly.

// Code for MarieSim and MarieSimEx ORG 100 Input // Read input Store N // N=input Store C // C=N Subt I // AC = N-1 SKIPCOND 800 // if N-1 > 0 JUMP L3 L2, Load B // AC=B ADD A // AC=B+A Store C // C=B+A Load B // AC=B Store A // A=B Load C // AC=C Store B // B=C Load I // AC=1 ADD One // AC=I+1 Store I // I=I+1 SUBT N // AC=I-N SKIPCOND 400 // if I=N, done Jump L2 // otherwise, continue L3, Load C // print result Output Halt // stop // Variable Declarations I, DEC 1 // index N, DEC 0 // N C, DEC 0 // f(N) B, DEC 1 // f(N-1) A, DEC 0 // f(N-2) One, DEC 1 // Used for increment by 1

// Code for MarieSimEx ORG 100 Input // Read input Store N // N=input Store C // C=N Subt I // AC = N-1 SKIPCOND 800 // if N-1 > 0 JUMP L3 L2, Load B // AC=B ADD A // AC=B+A Store C // C=B+A Load B // AC=B Store A // A=B Load C // AC=C Store B // B=C LIMM 1 // AC=1 ADD I // AC=I+1 Store I // I=I+1 SUBT N // AC=I-N SKIPCOND 400 // if I=N, done Jump L2 // otherwise, continue L3, Load C // print result Output Halt // stop // Variable Declarations I, DEC 1 // index N, DEC 0 // N C, DEC 0 // f(N) B, DEC 1 // f(N-1) A, DEC 0 // f(N-2)

Method 2 (Using Function and Global Variables): This method defines the computation part in the above code as a function called Fib. The program has the same variables as in above code. The function Fib gets input from N and save its result in C. The program gets input N first, then calls the function Fib, and finally prints the result C. Note that the subroutine call instruction JNS for MarieSim saves the return address at Fib and the first instruction of the function starts at Fib+1. The instruction JumpI Fib will allow the subroutine return. On the other hand, the subroutine call instruction JNS for MarieSimEx saves the return address in the stack and the first instruction of the function starts at Fib. The instruction JR will allow the subroutine return and remove the return address from the stack. Please also note that the calling routine and subroutine use global variables to pass the information between them.

// Code for MarieSim ORG 100 Input //Read input Store N //N=input JNS Fib //Call subroutine Fib Load C //Print result Output Halt //Terminate // Subroutine Fib Fib, HEX 0 //for storing return addr Load N Store C //C=N Subt I //AC = N-1 SKIPCOND 800 //if N-1 > 0 JUMP L3 L2, Load B //AC=B ADD A //AC=B+A Store C //C=B+A Load B //AC=B Store A //A=B Load C //AC=C Store B //B=C Load I //AC=1 ADD One //AC=I+1 Store I //I=I+1 SUBT N //AC=I-N SKIPCOND 400 //if I=N, done Jump L2 //otherwise, continue L3, JumpI Fib // Global Variable Declarations I, DEC 1 //index N, DEC 0 //N -- input to Fib C, DEC 0 //f(N)-- output from Fib B, DEC 1 //f(N-1) A, DEC 0 //f(N-2) One, DEC 1 //used for increment by 1

// Code for MarieSimEx ORG 100 Input //Read input Store N //N=input JNS Fib //Call subroutine Fib Load C //Print result Output Halt //Terminate // Subroutine Fib Fib, Load N Store C //C=N Subt I //AC = N-1 SKIPCOND 800 //if N-1 > 0 JUMP L3 L2, Load B //AC=B ADD A //AC=B+A Store C //C=B+A Load B //AC=B Store A //A=B Load C //AC=C Store B //B=C Limm 1 //AC=1 ADD I //AC=I+1 Store I //I=I+1 SUBT N //AC=I-N SKIPCOND 400 //if I=N, done Jump L2 //otherwise, continue L3, JR // Global Variable Declarations I, DEC 1 //index N, DEC 0 //N -- input to Fib C, DEC 0 //f(N)-- output from Fib B, DEC 1 //f(N-1) A, DEC 0 //f(N-2)

Method 3 (Using Function and Local Variables): This method will use local variables (I, A, B, C) inside the subroutine Fib. These local variables are allocated in the stack. Meanwhile, the input and output of the subroutine Fib are also passed via stack. The following tables show the values in stack at several important timestamps related to subroutines: (1) Right before calling Fib, (2) Right after calling Fib, (3) Right before Fib return, and (4) Right after Fib return.

(1) Right before calling Fib	Memory address	Used for
$	Mem[SP]	Input N

(2) Right after calling Fib	Memory address	Used for
$-1 $ $+1 $+2 $+3 $+4	Mem[SP]-1 Mem[SP] Mem[SP]+1 Mem[SP]+2 Mem[SP]+3 Mem[SP]+4	Input N Return address Local variable I Local variable A Local variable B Local variable C

(3) Right before Fib return	Memory address	Used for
$-1 $ $+1 $+2 $+3 $+4	Mem[SP]-1 Mem[SP] Mem[SP]+1 Mem[SP]+2 Mem[SP]+3 Mem[SP]+4	Output Fib(N) Return address Local variable I Local variable A Local variable B Local variable C

(4) Right after Fib return	Memory address	Used for
$	Mem[SP]	Output Fib(N)

As shown above, (1) Right before calling Fib, the main code pushes the input N on stack. Then the subroutine Fib is called. Note that when a subroutine is called, its return address is pushed on stack by the subroutine call instruction JNS. (2) Right after calling Fib, the return address is just put on top of stack. So, the value of stack pointer $ (or Mem[PS]) is creased by 1 and thus the input N is now located at $-1. Then the subroutine Fib uses four memory locations $+1, $+2, $+3, and $+4 from the stack area of memory space for its local variables I, A, B, and C, respectively. Therefore, the stack frame for the subroutine Fib consists of six memory words as shown in (2). (3) Right before the subroutine Fib returns, it stores the result Fib(N) in stack and overwrites the input N. Then it returns. Note that the subroutine return instruction JR will pop (remove) the return address from stack. (4) Right after the subroutine Fib returns, the return address is just removed from stack. So, the value of stack pointer $ (or Mem[PS]) is decreased by 1 and thus the result Fib(N) is now on top of stack (i.e. located at $). Then the main code pops the result into C. Finally, it prints the result. The assembly language code is shown as below.

//Main code for MarieSimEx

ORG 100

Input //Read input

Store N //N=input

Push N //Push N on stack (need to expand)

JnS Fib //Call subroutine Fib

Pop C //Pop result into C (need to expand)

Load C //print result

Output

Halt //terminate program

//Subroutine Fib

Fib, Limm 1

Store $+1 //I=1

Store $+3 //B=1

Limm 0

Store $+2 //A=0

load $-1 //AC=N

SUBT $+1 //N-1

SKIPCOND 800 //if N-1 > 0

JUMP L3

L2, Load $+3 //AC=B

ADD $+2 //AC=B+A

Store $+4 //C=B+A

Load $+3 //AC=B

Store $+2 //A=B

Load $+4 //AC=C

Store $+3 //B=C

Limm 1

ADD $+1 //AC=I+1

Store $+1 //I=I+1

SUBT $-1 //AC=I-N

SKIPCOND 400 //if I=N, done

Jump L2 //otherwise, continue

Load $+4 //AC=C

Store $-1 //Save result

L3, JR

//Global Variable Declarations

N, DEC 0 //N -- input to Fib

C, DEC 0 //f(N)-- output from Fib

Method 4 (Using Recursive Function): This method will implement the subroutine Fib as a recursive function. Like in the method 3, we are going to use the same memory location of stack to store both input N and output Fib(N). Before calling the function Fib, the input N must be on top of stack (i.e., it is located at $.), and after returning from function Fib, the result Fib(N) must be on top of stack as well. The stack contents before calling and after calling are illustrated by the following tables (1) and (8).

Because of Fib(N) = Fib(N-2) + Fib(N-1), we will need to call Fib(N-1) and Fib(N-2) inside Fib(N). Therefore, we need two more local memory spaces inside the stack frame of Fib(N) to store (N-1)/Fib(N-1) and (N-2)/Fib(N-2). We always need one stack space for the return address. So, the stack frame for Fib(N) needs four memory spaces on as illustrated in the following tables from (2) to (7).

(1) Right before calling Fib(N)	Memory address	Used for
$	Mem[SP]	Input N

(2) Right after calling Fib(N)	Memory address	Used for
$-1 $+0 $+1 $+2	Mem[SP]-1 Mem[SP] Mem[SP]+1 Mem[SP]+2	Input N Return address of Fib(N)

(3) Right before calling Fib(N-1)	Memory address	Used for
$-2 $-1 $ $+1	Mem[SP]-2 Mem[SP]-1 Mem[SP] Mem[SP]+1	Input N Return address of Fib(N) N-1

(4) Right after Fib(N-1) return	Memory address	Used for
$-2 $-1 $ $+1	Mem[SP]-2 Mem[SP]-1 Mem[SP] Mem[SP]+1	Input N Return address Fib(N-1)

(5) Right before calling Fib(N-2)	Memory address	Used for
$-3 $-2 $-1 $	Mem[SP]-3 Mem[SP]-2 Mem[SP]-1 Mem[SP]	Input N Return address Fib(N-1) N-2

(6) Right after Fib(N-2) return	Memory address	Used for
$-3 $-2 $-1 $	Mem[SP]-3 Mem[SP]-2 Mem[SP]-1 Mem[SP]	Input N Return address Fib(N-1) Fib(N-2)

(7) Right before Fib(N) return	Memory address	Used for
$-1 $ $+1 $+2	Mem[SP]-1 Mem[SP] Mem[SP]+1 Mem[SP]+2	Fib(N) Return address Fib(N-1) Fib(N-2)

(8) Right after Fib(N) return	Memory address	Used for
$	Mem[SP]	Fib(N)

You may notice immediately that the value of $ in tables (2) - (7) changes from time to time after running certain instructions. As you may already notice that $ will be increased by 1 after running JNS instruction and decreased by 1 after running JR. In addition, you can increase or decrease the value of $ or Mem[SP] very easily. Because SP is a reserved memory address (label), you can use SP in your program like any other addresses (labels). For example, if you want to increase the value of $ by 5, you can perform the following three instructions.

Limm 5

Add SP

Store SP

As shown below, the main code is the same as that in method 3. Right after calling Fib(N), the stack frame is shown as in the above table 2. If N 1, it is done. Otherwise, store N-1 at $+1 and increase $ by 1. Now, N-1 is at $ as shown in the above table 3 and is ready to call Fib(N-1). Right after Fib(N-1) returns, its result Fib(N-1) is stored at $ as shown in the above table 4. Then store N-2 at $+1 and increase $ by 1. Now N-2 is at $ as shown in the above table 5 and is ready to call Fib(N-2). Right after Fib(N-2) returns, the result Fib(N-2) is stored at $ as shown in the above table 6. Then $ is restored by decreasing by 2. Next, the result Fib(N) = Fib(N-1) + Fib(N-2) is computed and stored at $-1 as shown in the above table 7. Now it is ready for Fib(N) to return. After the return, Fib(N) is at $ as shown in the above table 8 because the return instruction JR decreases $ by 1. The assembly code is shown as below. Different colors are applied for different stages of the code as described in the above.

//Main code for MarieSimEx

ORG 100

Input //Read input

Store N //N=input

Push N //Push N on stack (need to expand)

JnS Fib //Call subroutine Fib

Pop C //Pop result into C (need to expand)

Load C //print result

Output

Halt //terminate program

//Subroutine Fib

Fib, Limm -1

Add $-1 // AC = N-1

Skipcond 800 // if N > 1

jump L1 // done

Store $+1 // store N-1 to $+1

Limm 1 // AC = 1

Add SP // AC = SP + 1

Store SP // Increase SP ($) by 1

JNS Fib // Call F(N-1)

Limm -2 // AC = -2

Add $-2 // AC = N-2

Store $+1 // Store N-2 to $+1

Limm 1 // AC = 1

Add SP // AC = SP + 1

Store SP // Increase SP ($) by 1

JNS Fib // Call F(N-2)

Limm -2 // AC = -2

Add SP // AC = SP-2

Store SP // restore SP (decrese by 2)

Load $+1 // AC = Fib(N-1)

ADD $+2 // AC = F(N-1) + F(N-2) = F(N)

Store $-1 // store Fib(N) to $-1

L1, JR

//Global Variable Declarations

N, DEC 0 //N -- input to Fib

C, DEC 0 //f(N)-- output from Fib

Programming Assignments

Two programming assignments are given as below.

PA1: Add all positive integers in a given array and print the sum. A skeleton code is given and can be downloaded here (array_skeleton.mas). Note that the extension name of the skeleton file is .txt. You should change it back to .mas in order to assemble and run the code.

PA2: Multiply two integers entered from keyboard and print the product. As MARIE architecture does not have multiplication instruction, we have to use addition to compute multiplication. A formular for this computation is given as below.

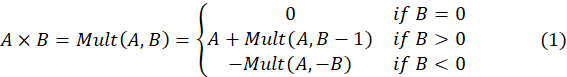
When B is a non-negative integer, then

(2)

The following C++ code shows to compute multiplication of two integers by using the formular (2). It gets two input integers X and Y from the keyboard. Then compute the absolute value of Y and save it in Z. Next, compute the product of X and Z and save it in C by using a loop based on formular (2). Next, if Y < 0, then the final product should be -C. Finally print result.

int main(){

int X, Y, Z, C;

cout << "Please enter two integers:" << endl;

cin >> X >> Y;

// Z = absolute value of Y

if (Y < 0)

Z = -Y;

else

Z = Y;

// C = product of X and Z

C = 0;

while (Z>0)

{

C = C + X;

Z = Z - 1;

}

// If Y < 0, then C = -C

if (Y < 0)

C = -C;

cout << C << endl; // Print result

return 0;

}

PA2.A: Your assignment is to convert the above C++ code into a MARIE assembly language code. A skeleton code is given here (MultLoopSkeleton.mas). You just need to fill in a part of code that computes the product of X and Z by using a while loop.

The following C++ code shows to compute multiplication of two integers by using the formular (2). It is the same with the above C++ code except it uses a function to the product of X and Z.

int main(){ int X, Y, Z, C; cout << "Please enter two integers:" << endl; cin >> X >> Y; // Z = absolute value of Y if (Y < 0) Z = -Y; else Z = Y; C = Mult(X, Z); // If Y < 0, then C = -C if (Y < 0) C = -C; cout << C << endl; return 0;

// Return the product of A and B, // where A is an integer and // B is a non-negative integer int Mult(int A, int B) { int P; P = 0; while (B > 0) { P = P + A; B = B - 1; } return P; }

PA2.B: Your assignment is to convert the above C++ code into a MARIE assembly language code. A skeleton code is given here (MultFuncSkeleton.mas). You just need to fill in a part of code that computes the product of X and Z by using a function. That is to write a subroutine called Mult. Note that you need to use stacks that will hold the function’s inputs as and output as well as the return address. MarieSimEx should be used.

PA2.C: (Bobus) Like in PA2.B, but you need to implement the subroutine Mult as a recursive function. You can use the same skeleton file in PA2.B and then rename it as MultRecFuncSkeleton.txt. Note that MarieSimEx must be used. A C++ recursive function Mult is shown as below for your reference.

// Recursive function

// Return the product of A and B,

// where A is an integer and B is a non-negative integer

int Mult(int A, int B)

{

int P;

if (B == 0)

P = 0;

else

P = A + Mult(A, B-1);

return P;

}