(Latest Revision: Nov 23, 2021)

Solution to the 2022 Flow Network Problem

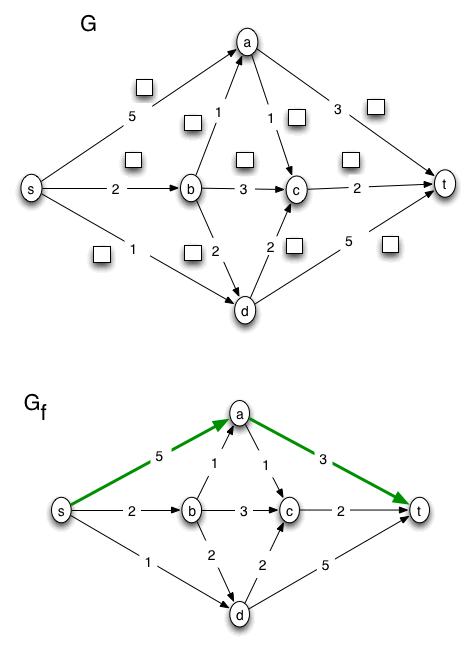
flow problem solution, page 01
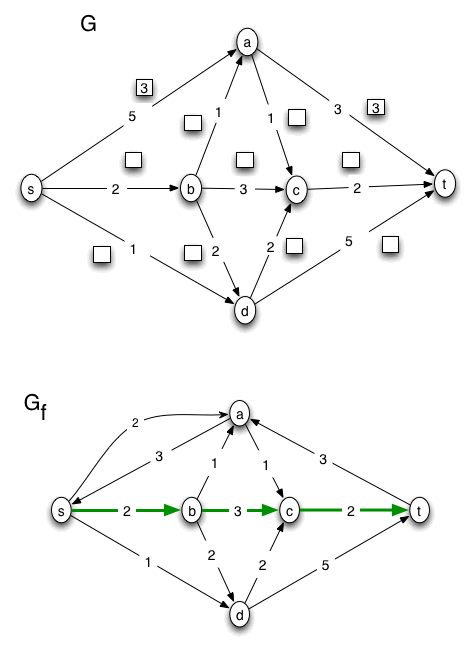
flow problem solution, page 02
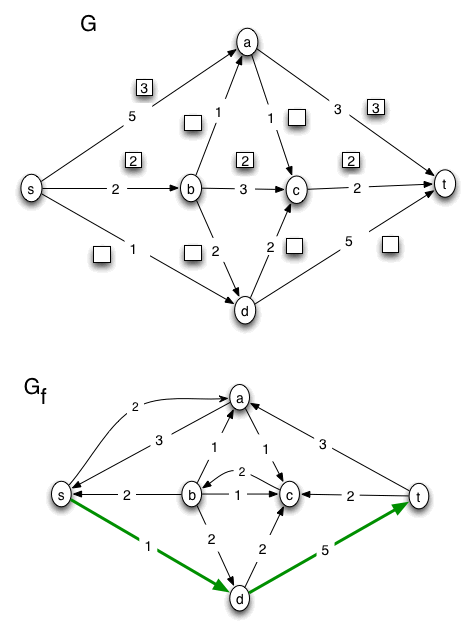
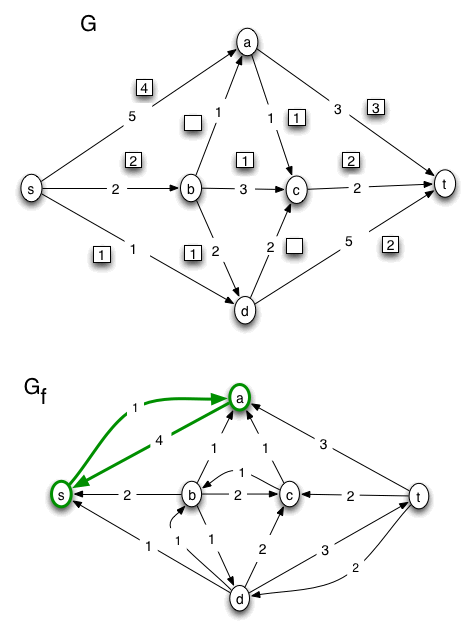
flow problem solution, page 03
flow problem solution, page 03
flow problem solution, page 03

For this problem, the A side of the minimum cut is {s, a}. No other nodes are reachable from s in the final version of the residual graph, Gf. The capacity of the cut is the sum of the capacities of the edges (in G) leaving the A side of the cut, 3 + 1 + 2 + 1 = 7. The value of the max flow is the sum of the flows on the edges leaving the source node s in G. That sum is 4 + 2 + 1, which also equals 7. These calculations verify that the max value of an s-t flow is equal to the min capacity of an s-t cut, which, according to the "Max-Flow, Min-Cut Theorem," is true for any flow network.