(Latest Revision:
Nov 23, 2021)
Flow Network Problem
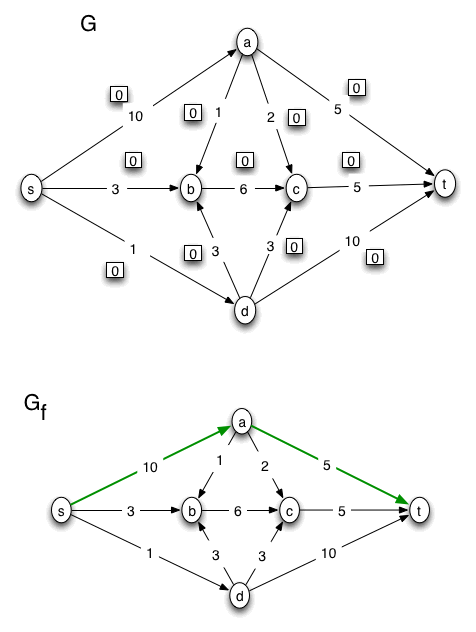
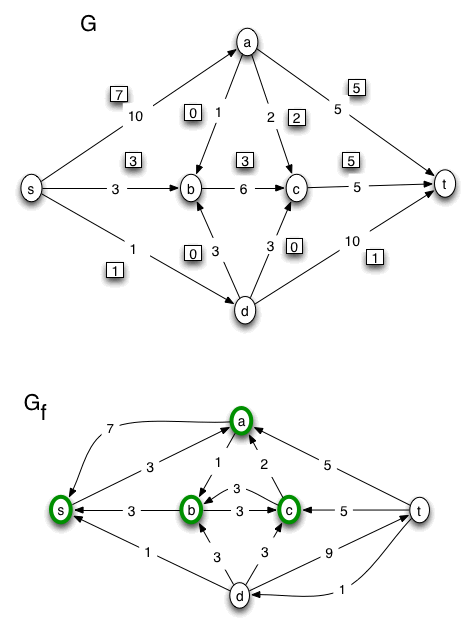
On display below is an example of how to use the Ford-Fulkerson Algorithm to find a max flow and min cut in a flow network. To review the algorithm, have a look at the information about it in the text book, or watch my screencast here.
In the diagrams, edges are labeled with capacities, and flows on edges are depicted as numbers written in squares. In the first diagram we start with the flow network G with all the squares containing zero, representing the zero flow. In the second diagram, we create the residual graph, Gf, corresponding to the flow in the previous diagram of G.
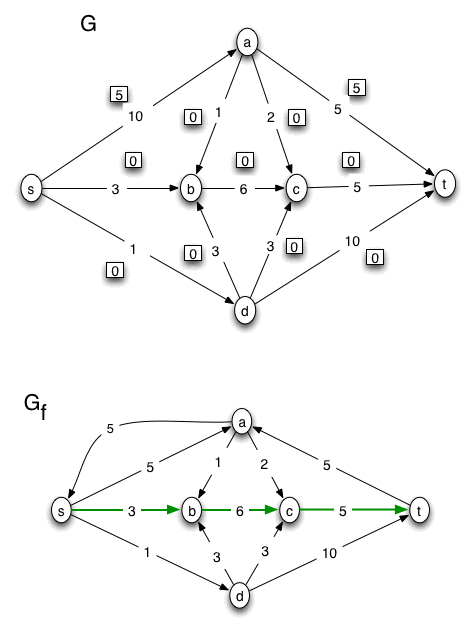
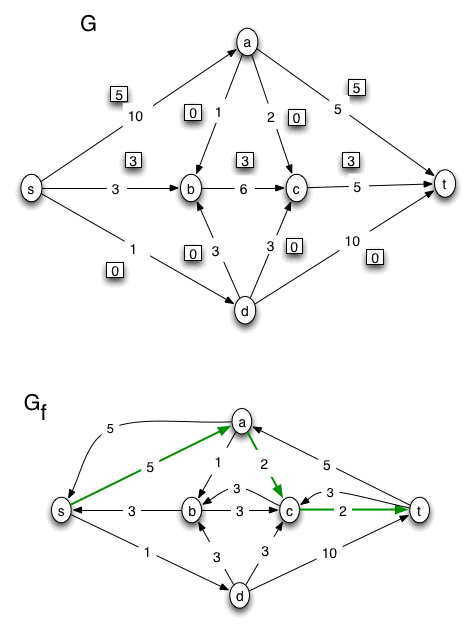
After that we perform this loop:
WHILE there is a path, P, in Gf from the source to the sink
- mark such a path P in Gf
- make a next copy of G, showing the new flow, as obtained by augmenting the previous flow using the path P
- create the next copy of the residual graph, Gf, corresponding to the flow in the latest diagram of G.
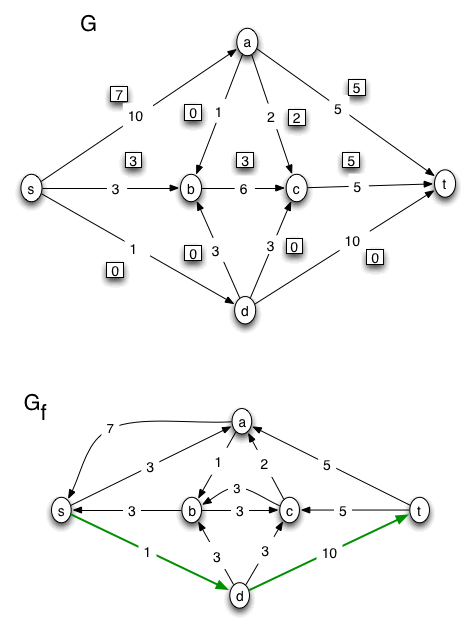
The last copy of Gf will be one in which there is no path from the source to the sink. In that copy of Gf, we mark the nodes that are reachable by a path from the source. Those nodes determine a minimal cut in G.
How We Figure The Max Flow and Min Capacity
Note that the value of the max flow found, v(f*), can be read off from the final version of G. It is equal to the sum of the flows on edges leaving the source: v(f*) = 7 + 3 + 1 = 11. Note also that the capacity of the minimum cut is 5 + 5 + 1 = 11 = v(f*). (According to the "Max-Flow, Min-Cut Theorem," in any flow network, the max value of an s-t flow is equal to the min capacity of an s-t cut. )
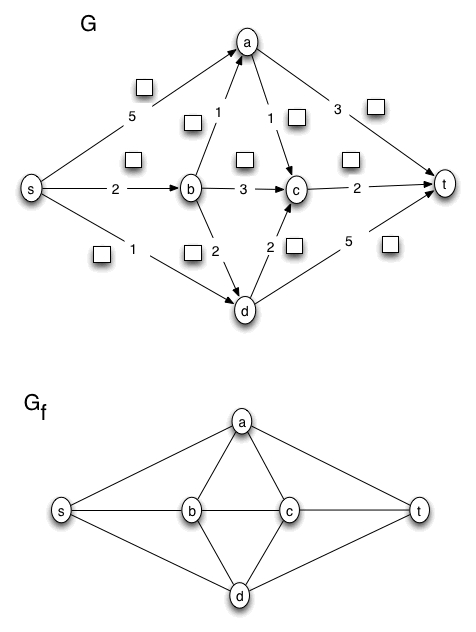
YOUR ASSIGNED PROBLEM:
Work the problem in the figure below using copies of the worksheet shown. Do the problem in the same way as the example above is done.
Below are links to GIF, JPEG, TIFF, and PDF versions of the worksheet, for your convenience. If you have access to a printer, you can print out copies to use as you work the problem.
the GIF version
the JPG version
the TIFF version
the PDF version
Directions For Doing The Problem:
To keep things simple, I want you to turn in this assignment in person, in class.
- Do the problem on a series of copies of the worksheet, in the same manner in which the example problem above is done.
- On the final worksheet in the series, be sure to highlight the nodes in Gf that are still reachable from the source node, s.
- Also, on the final worksheet, use the final version of G, to
- figure the value of the maximum flow on G,
- figure the capacity of the minimum cut of G, and
- verify that the value of the max flow equals the capacity of the min cut.
(If the two aren't equal, you did something wrong.)
- If you need help figuring the max flow and min capacity, re-reading the section above entitled "How We Figure The Max Flow and Min Capacity" should help, and also you can review text, notes, and recorded lectures to go over the definitions and concepts.
To turn in the assignment, number the sheets, attach them together in order, and place them on my desk as you come in at the beginning of class.





