(Latest Revision:
Nov 04, 2021)
CS 4440 Dijkstra's Algorithm Practice Problem
Some Background
Here is an an adjacency matrix that represents a directed graph, G1:
"from node"
numbers "to node" numbers -->
| 1 2 3 4 5
| 1 . 50 30 100 10
V 2 . . . . .
3 . 5 . . .
4 . 20 50 . .
5 . . . 10 .
Each number in the matrix represents an edge of G1. For example the "50" in row 4, column 3 represents an edge of G1 that starts at node 4 and goes to node 3.
Look
here
at how to perform Dijkstra's algorithm, using the adjacency matrix data above, to find the lengths of all the shortest paths from the source node (node #1) to the other nodes, as well as the paths themselves.
When you click on the link above, you see that tabular information just like this is created to solve the problem:
Part One of The Solution:
Step v C BackPoint Dist
1 2 3 4 5 1 2 3 4 5
Init -- {2,3,4,5} [X,1,1,1,1] [0,50,30,100,10]
1 5 {2,3,4} [X,1,1,5,1] [0,50,30, 20,10]
2 4 {2,3} [X,4,1,5,1] [0,40,30, 20,10]
3 3 {2} [X,3,1,5,1] [0,35,30, 20,10]
The "Dist" information in the table tells us that the shortest paths from the start node to nodes 2, 3, 4, and 5, are of lengths 35, 30, 20, and 10.
From the BackPoint table, we can also determine what all the actual shortest paths are from the start node to the other nodes. That works as follows.
Part Two of The Solution:
The back pointer of 2 is 3 and the back pointer of 3 is 1.
Therefore the shortest path to 2 is 2 <== 3 <== 1.
The back pointer of 3 is 1.
Therefore the shortest path to 3 is 3 <== 1.
The back pointer of 4 is 5, the back pointer of 5 is 1.
Therefore the shortest path to 4 is 4 <== 5 <== 1.
The back pointer of 5 is 1.
Therefore the shortest path to 5 is 5 <== 1.
When you understand Dijkstra's Algorithm and the implementations we covered in class, you will be able to generate a tabular solution to the problem like the one above with relative ease, using only an adjacency matrix for your input.
There are some other presentations in the notes that explain the algorithm using "pictures." They are here and here, and there is pseudo-code for the algorithm here.
The Assignment
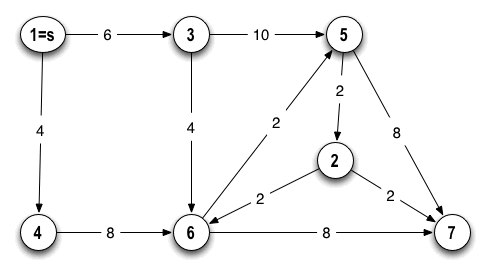
Here is an adjacency matrix representing a different graph, G2.
"from"
node # "to" node #
1 2 3 4 5 6 7
1 . . 6 4 . . .
2 . . . . . 2 2
3 . . . . 10 4 .
4 . . . . . 8 .
5 . 2 . . . . 8
6 . . . . 2 . 8
7 . . . . . . .
Using the information about G2 above as an input to Dijkstra's algorithm, produce exactly the same kind of solution information for G2 as illustrated by parts one and two of the solution of the G1 example problem above.
Thus, you will be executing Dijkstra's algorithm (by hand) on G2, and you will be finding all the shortest paths from the start node in G2 to all the other nodes, and their lengths. (Assume that node #1 is the start node.)
Note: The important thing here is that you get as close to possible to creating the output information correctly by using the adjacency matrix information. It's a way to show your understanding of the details of the algorithm.
I'm including below a diagram of G2. However, don't forget that your goal is to be able to execute the algorithm like a computer would - using only the adjacency matrix as input. It's quite possible that, on a quiz, you can get a problem like this, and there may not be a "picture" of the graph to go with it. You may be given only the adjacency matrix of a graph, or maybe an edge-list representation.
Directions For Submitting Solution:
- Prepare your solution to the problem (both parts one and two).
- COPY AND PASTE the text of your solution into an e-mail.
- DO NOT attach a file to your e-mail.
- DO copy and paste the text of your solution into the message window of the e-mail.
- DO Make the following exact text the subject line of your e-mail.
CS 4440 Dijkstra's Algorithm Problem
- DO copy the exact text above and & PASTE IT IN as the subject line of your e-mail
to make sure it is correct.
- Get it right, or get no credit!
- Send the E-mail to tester2@cs.csustan.edu
