(Latest Revision:
Feb 27, 2021)
CS 4440 Dijkstra's Algorithm Practice Problem
Some Background
Here is an an adjacency matrix that represents a directed graph, G1:
"from"
node # "to" node #
1 2 3 4 5
1 . 50 30 100 10
2 . . . . .
3 . 5 . . .
4 . 20 50 . .
5 . . . 10 .
Each number in the matrix represents an edge of G1. For example the "50" in row 4, column 3 represents an edge of G1 that starts at node 4 and goes to node 3.
Look
here
at how to perform Dijkstra's algorithm, using the adjacency matrix data above, to find the lengths of all the shortest paths from the source node (node #1) to the other nodes, as well as the paths themselves.
When you click on the link above, you see that tabular information just like this is created to solve the problem:
Step v C BackPoint Dist
2 3 4 5 2 3 4 5
Init -- {2,3,4,5} [X,1,1,1,1] [0,50,30,100,10]
1 5 {2,3,4} [X,1,1,5,1] [0,50,30, 20,10]
2 4 {2,3} [X,4,1,5,1] [0,40,30, 20,10]
3 3 {2} [X,3,1,5,1] [0,35,30, 20,10]
The information in the table tells us that the shortest paths to nodes 2, 3, 4, and 5, are of lengths 35, 30, 20, and 10. The information also tells us that the shortest paths are 1->3->2, 1->3, 1->5->4, and 1->5.
When you understand Dijkstra's Algorithm and the implementations we covered in class, you will be able to generate a tabular solution to the problem like the one above with relative ease, using only an adjacency matrix for your input.
There are some other presentations in the notes that explain the algorithm using "pictures." They are here and here, and there is pseudo-code for the algorithm here.
The Assignment
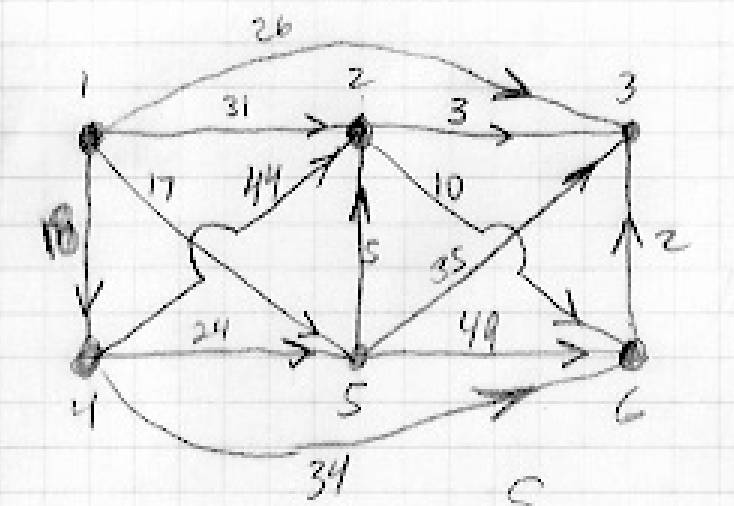
Here is an adjacency matrix representing a different graph, G2.
"from"
node # "to" node #
1 2 3 4 5 6
1 . 31 26 18 17 .
2 . . 3 . . 10
3 . . . . . .
4 . 44 . . 24 34
5 . 5 35 . . 49
6 . . 2 . . .
Using the information about G2 above as an input to Dijkstra's algorithm, make the same kind of table of output information for G2 as the example output table above for G1. Thus, you will be executing Dijkstra's algorithm (by hand) on G2, and you will be finding the shortest paths and their lengths. (Assume that node #1 is the start node.) Also, in your answer, report on what the actual shortest paths are, in the same way that I gave the information in my sample solution.
Note: The important thing here is that you get as close to possible to creating the output table correctly by using the adjacency matrix information. It's a way to show your understanding of the details of the algorithm.
I'm including below a diagram of G2. However, don't forget that your goal is to be able to execute the algorithm like a computer would - using only the adjacency matrix as input.
Directions For Submitting Solution:
Prepare your solution to the problem.
COPY AND PASTE the text of your solution into an e-mail.
DO NOT ATTACH A FILE.
COPY AND PASTE the text into the message window of the e-mail.
Make this exact text the subject line of your e-mail:
CS 4440 Dijkstra's Algorithm Problem
Copy the exact text above and & paste it in as the subject line
to make sure it is correct.
Get it right, or get no credit.
Send the E-mail to
tester2@cs.csustan.edu
