(Latest Revision:
Feb 20, 2019)
Dijkstra's Algorithm Practice Problem
Some Background
Look at how Dijkstra's algorithm is run with "paper and pencil"
here.
The link above points to a page where you see this tabular display:
Step v C BackPoint Dist
Init -- {2,3,4,5} [X,1,1,1,1] [0,50,30,100,10]
1 5 {2,3,4} [X,1,1,5,1] [0,50,30,20,10]
2 4 {2,3} [X,4,1,5,1] [0,40,30,20,10]
3 3 {2} [X,3,1,5,1] [0,35,30,20,10]
The display above shows, step-by-step, how Dijkstra's algorithm finds the lengths of all the shortest paths from a source node to all the other nodes in a graph. The graph is pictured on the page with the table. The version of Dijkstra's algorithm used also (implicitly) finds all the shortest paths. The "BackPoint" list contains sufficient information to quickly construct all the shortest paths explicitly.
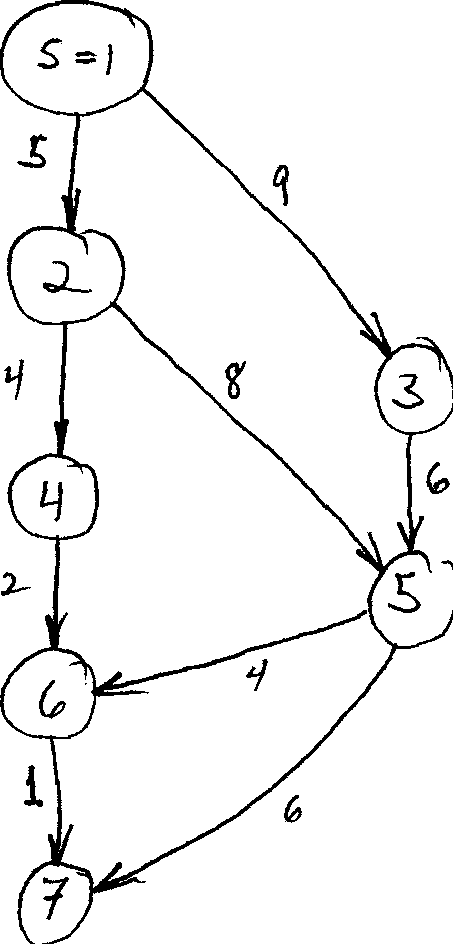
The Assignment
Using the graph below as an input to Dijkstra's algorithm, make the same kind of table for that graph. Thus, you will be executing Dijkstra's algorithm (by hand) on the graph below, and you will be finding the shortest paths and their lengths. (Assume the node with label "s=1" is the start node.)
Note: The important thing here is that you create the table correctly, with all the correct entries in all the right places. Doing that shows you understand the steps of the algorithm.