Notes On Chapter Eight -- Reliability And Channel Coding

• 8.1 Introduction
  
  
  • Techniques to control errors
  • Utilized in protocols at many levels
  
  
• 8.2 The Three Main Sources of Transmission Errors
  
  
  1. Interference
     
     
  2. Distortion
     • In optical fibers, some photons reflect off the cladding more than others, so travel further and take more time. So a pulse of light may exit the fiber more spread out than when it entered. This is a form of distortion called dispersion.
     • Copper wire has capacitance and inductance that causes it to tend to block signals at certain frequencies.
     • Placing a wire near a large metal surface can change the frequencies it blocks or allows.
     
     
  3. Attenuation - signals become weaker as they travel farther down a wire, fiber, or other medium.
  
  
  • Although some errors in transmitted information are inevitable, most can be detected and even corrected automatically.
  • The disadvantage of error detection/correction is that additional information must be created and added to what is transmitted, which means extra work and time.
  
  
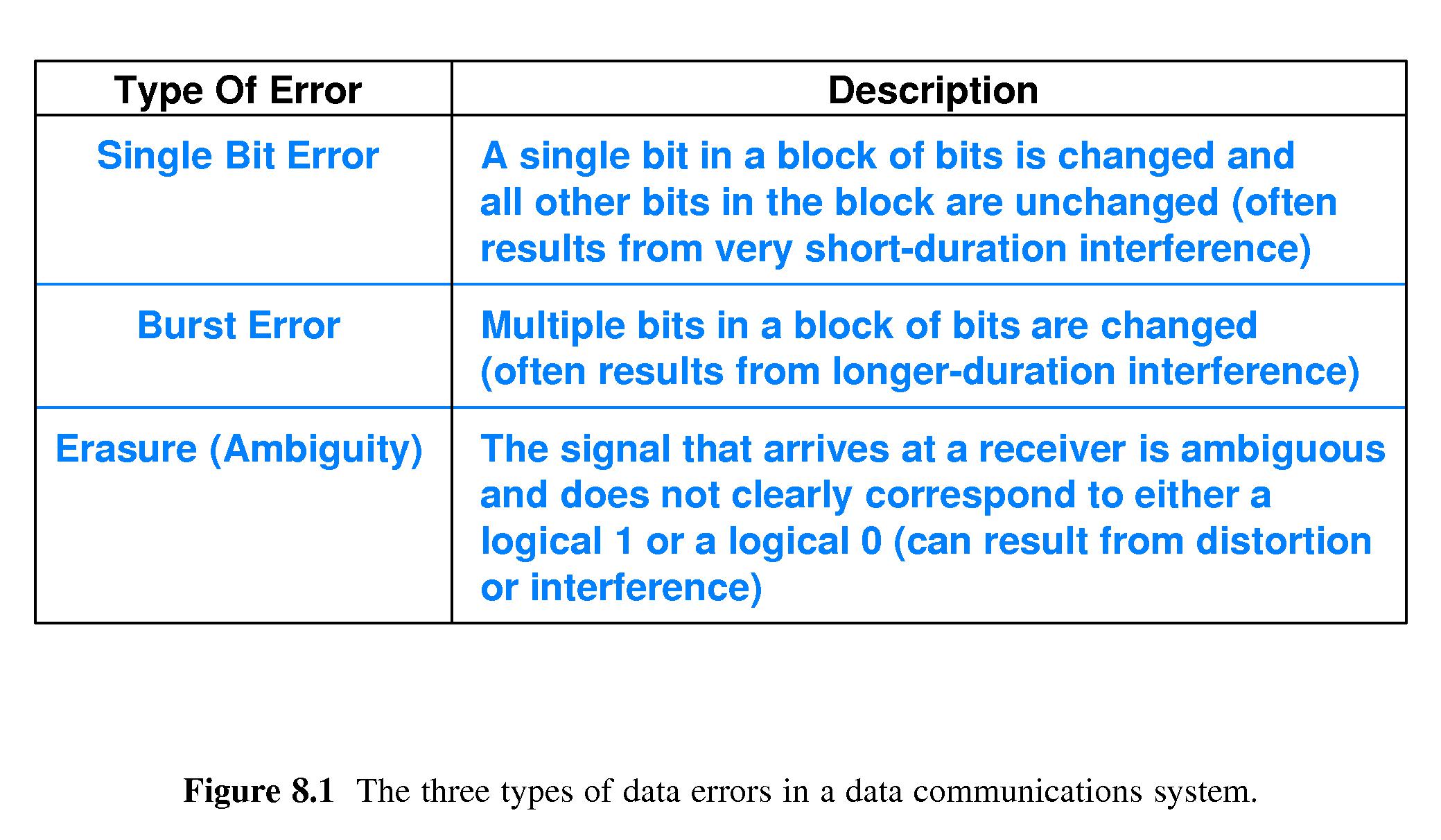
• 8.3 Effect of Transmission Errors on Data
  
  
  1. Single bit error - often caused by a 'spike' of interference.
     
     
  2. Burst Error - multiple bits in a block changed - often due to longer-duration interference.
     
     
  3. Erasure (Ambiguity) - signal does not clearly correspond to a 1 or 0 - often the result of distortion or interference
  
  
  
  
• 8.4 Two Strategies For Handling Channel Errors
  
  
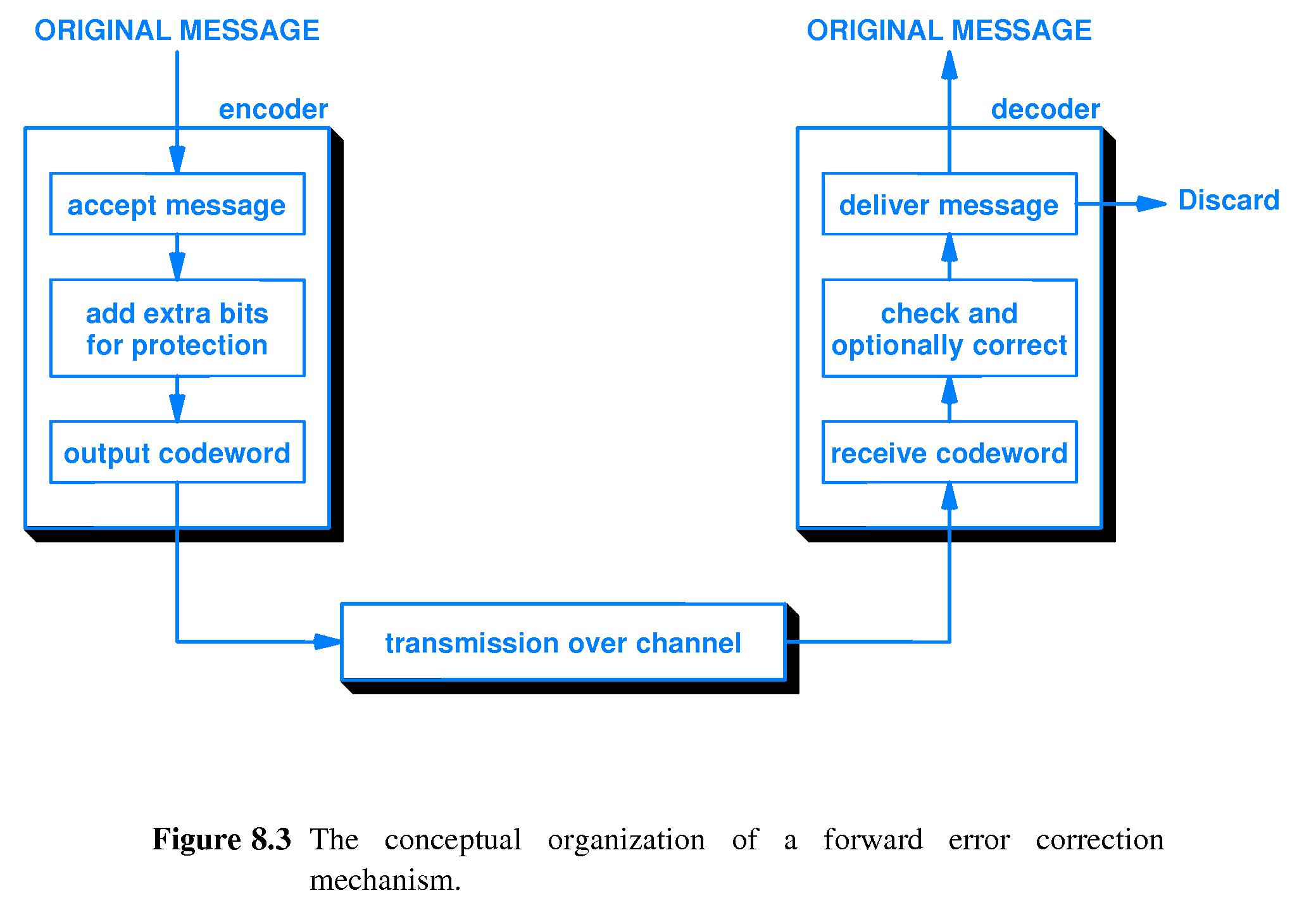
  • Forward Error Correction mechanisms - add information that allows receiver to detect and possibly correct errors.
    
    
  • Automatic Repeat reQuest (ARQ) mechanisms - add information that allows receiver to detect that an error has occurred and request that information be re-sent.
  
  
  
  
• 8.5 Block and Convolutional Error Codes
  
  
  • Block Error Codes
    • divide data into blocks
    • calculate a code from the bits in a block
    • attach it to the block (redundancy)
    
    
  • Convolutional Error Codes
    • compute a code over the entire data series
    • the code computed for a set of bits depends on the current input and some of the previous bits in the stream.
    
    
  • Convolution codes typically require more computation, but make detection of errors more likely.
  
  
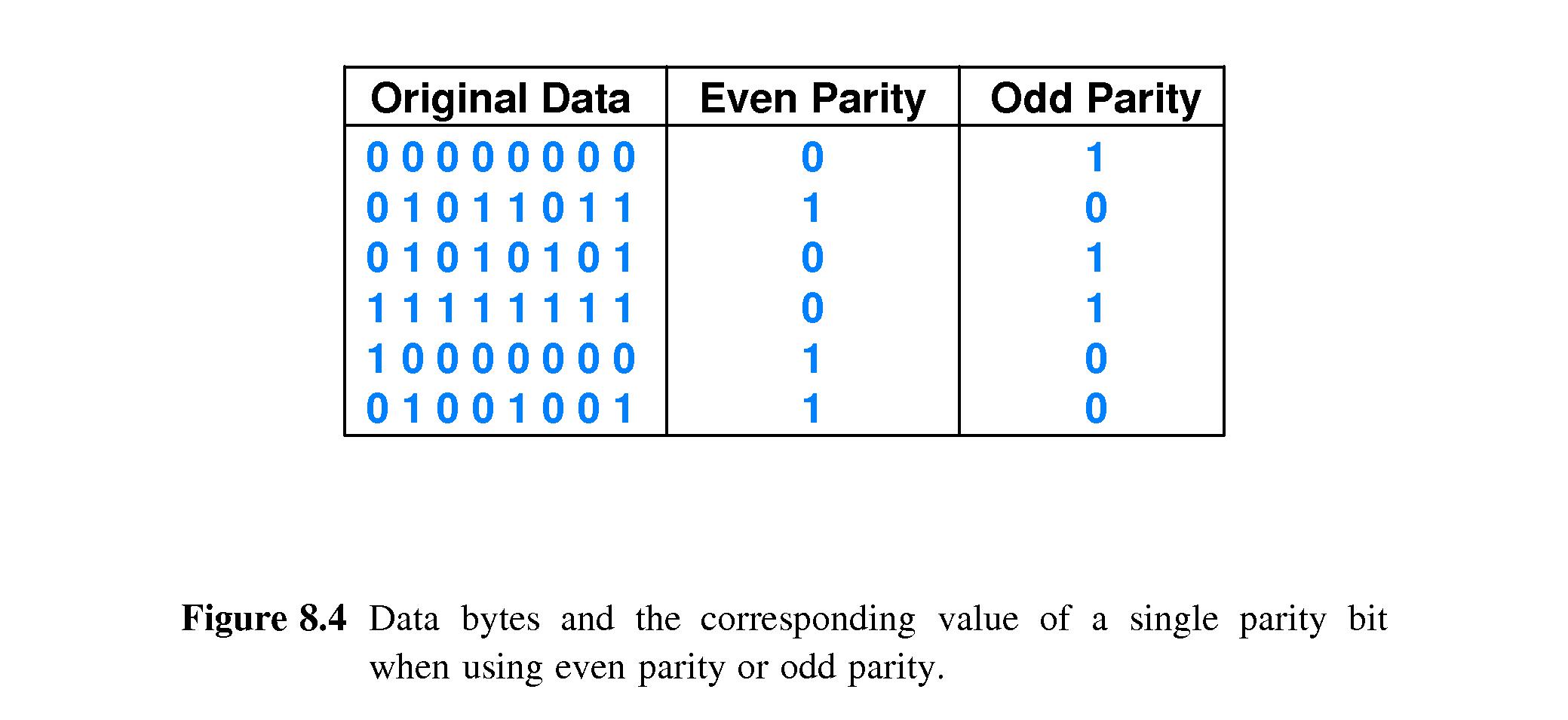
• 8.6 An Example Block Error Code: Single Parity Checking
  
  
  • Example:
    • Sender adds one bit to each byte.
    • Even parity: the added bit is 1 if the byte has an odd number of 1's, else 0.
  • The receiver can detect, but not correct, cases where an odd number of bits have changed during transmission.
  
  
  
  
• 8.7 The Mathematics of Block Error Codes and (n,k) Notation
  
  
  • Suppose there are n = k + r bits in each "codeword" -- k bits of data and r bits "redundancy"
  • Ideally, of the 2ⁿ possible strings of n bits, only a relatively few of them are valid codewords. (Typically there would be only 2^k codewords.)
  • Ideally common errors will transform valid code words into invalid code words, because such errors are detectable.
  • Example: with single (even) parity checking, n = 8 + 1 = 9. The valid codewords are those with an even number of 1-bits. Errors in a single bit tend to be more likely than other errors. Errors in a single bit transform a valid codeword into an invalid codeword, which is easily detected.
  
  
• 8.8 Hamming Distance: A Measure of a Code's Strength
  
  
  • Given two bit strings of equal length, the Hamming distance between them is defined to be the number of bit positions in which they differ.
  
  
  
  
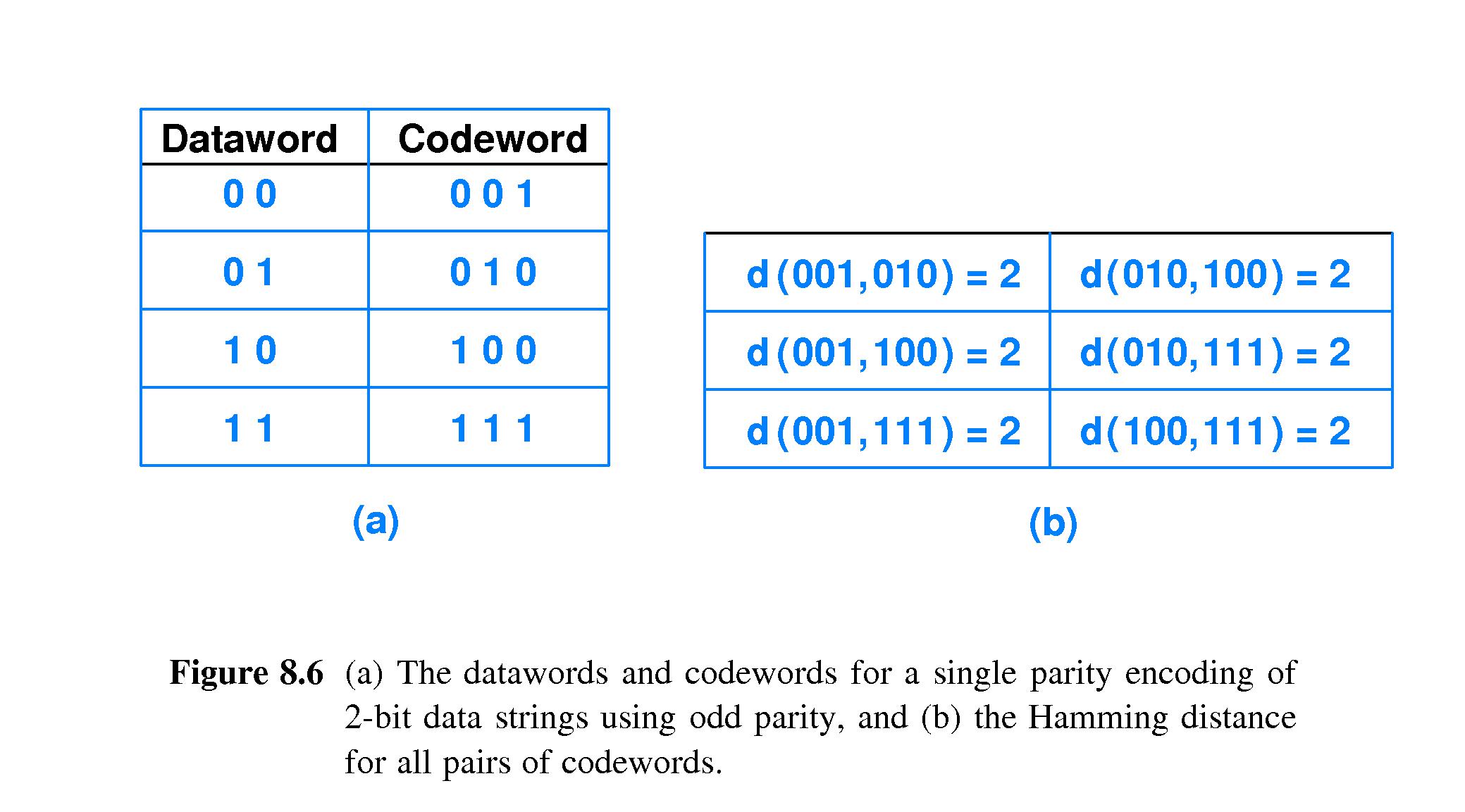
• 8.9 The Hamming Distance Among Strings in a Codebook
  
  
  • The minimum number of bit changes that can transform a valid codeword into another valid codeword is the same as the minimum Hamming distance between all pairs of valid codewords.
  
  
  
  
• 8.10 The Tradeoff Between Error Detection and Overhead
  
  
  • If the minimum Hamming distance is d_min then the receiver will always be able to figure out that a codeword has been damaged if it has between 1 and d_min-1 bit errors.
  • For that reason, it's good for d_min to be large.
  • However to make d_min larger, typically means having to add more bits of redundancy, which makes messages larger, which means it takes longer to send them, and requires more room to store them.
  • You need more time to send more redundancy bits, and more room to store them.
  
  
• 8.11 Error Correction with Row and Column (RAC) Parity
  
  
  • There are various schemes, not only for detecting, but also figuring out how to correct some possible errors.
  • Hamming codes use the idea of replacing an invalid word with the closest valid codeword. If the number of incorrect bits is less than half of d_min then the replacement corrects the error.
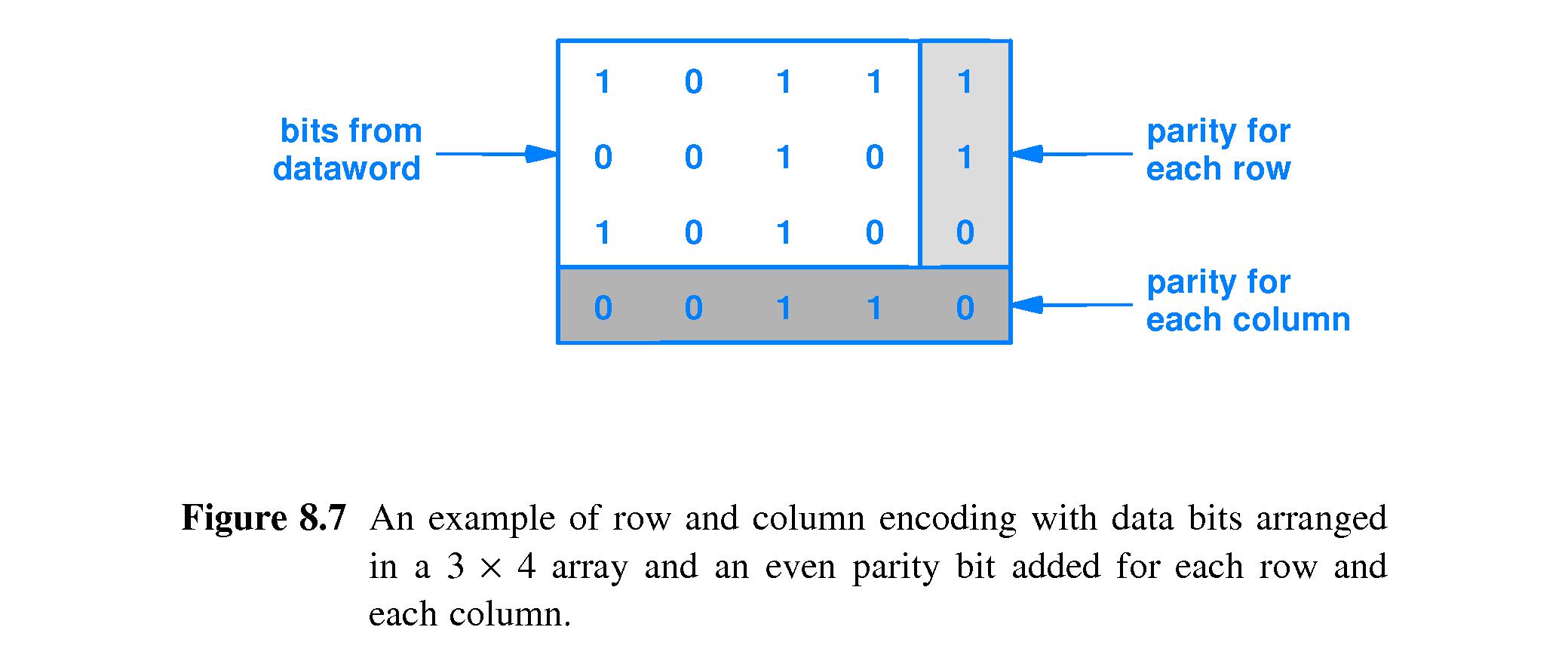
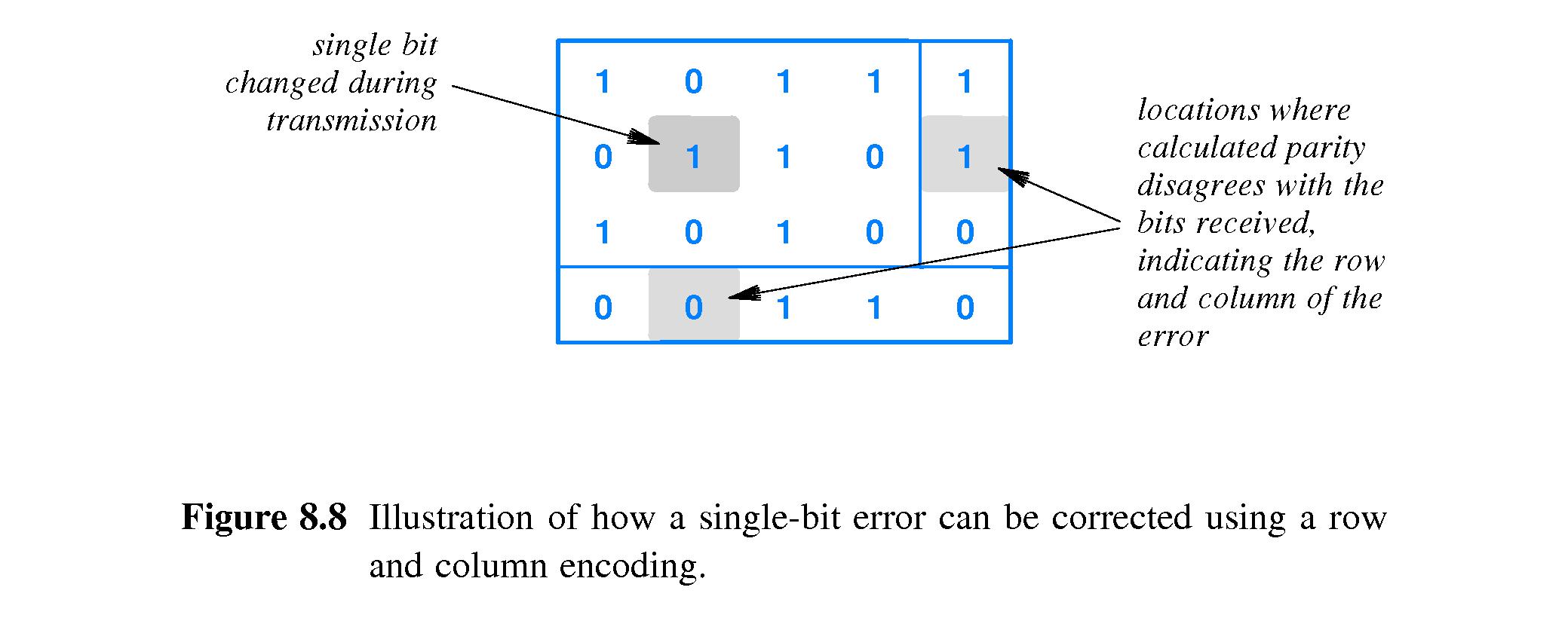
  • The textbook uses the example of a 12 bit codeword written as a 3X4 array of bits, each row and column having a parity bit associated. If exactly one bit is in error, the corresponding row and column parity bits will not be the same as the ones calculated by the receiver. Thus the receiver can infer the position of the incorrect bit.
  • It is important to understand that the "error-correction" may be wrong, depending on the actual nature of the error.
  
  
  
  
  
  
• 8.12 The 16 Bit Checksum Used in the Internet
  
  
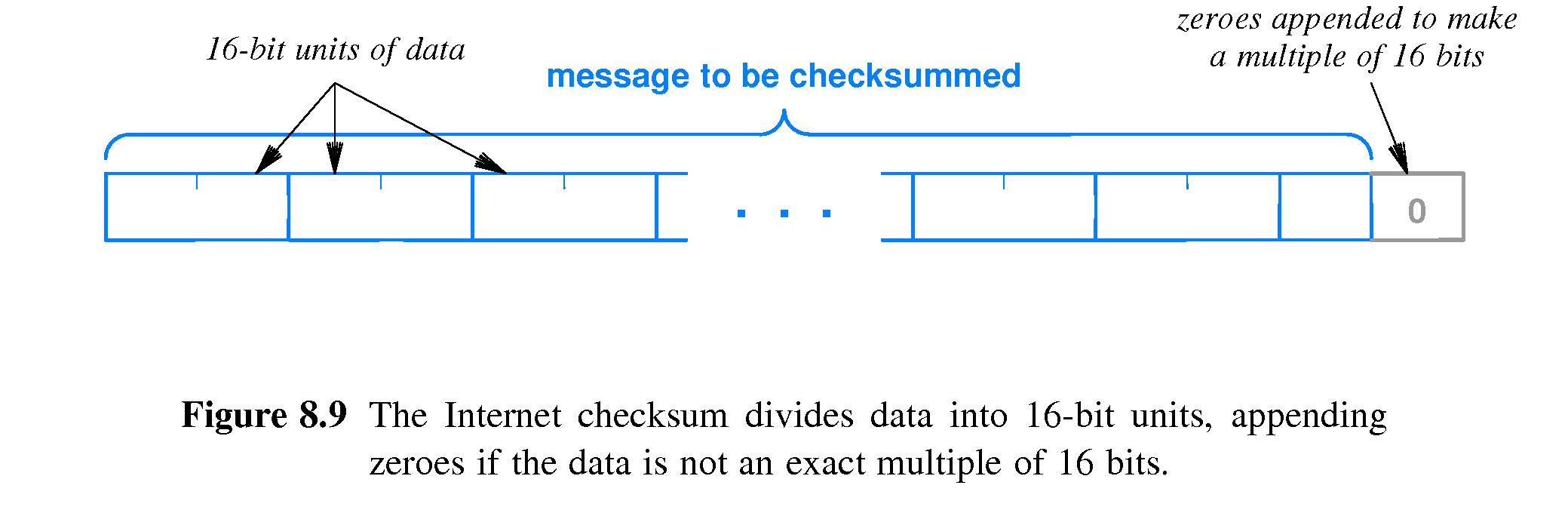
  • Basically the sender treats the message as a series of 16-bit numbers and computes the checksum by adding all those numbers.
  • There are additional minor details of how the algorithm works.
  • The sender sends the message, plus the checksum, to the receiver.
    
    
  • The receiver adds up the 16-bit numbers like the sender did, and also adds on the received checksum. The answer is supposed to be zero.
  • This makes it easy for the receiver to check for an error in the message.
  
  
  
  
  
  
• 8.13 Cyclic Redundancy Codes (CRCs)
  
  
  • CRC's are used in high-speed data networks
  • They can be applied to messages of arbitrary length
  • They have excellent error detection capability
  • They can be computed quickly
  • Learning to understanding the structure of CRC's and the algorithms for generating CRC's is worthwhile, but beyond the scope of this course.
  
  
• 8.14 An Efficient Hardware Implementation of CRC
  
  
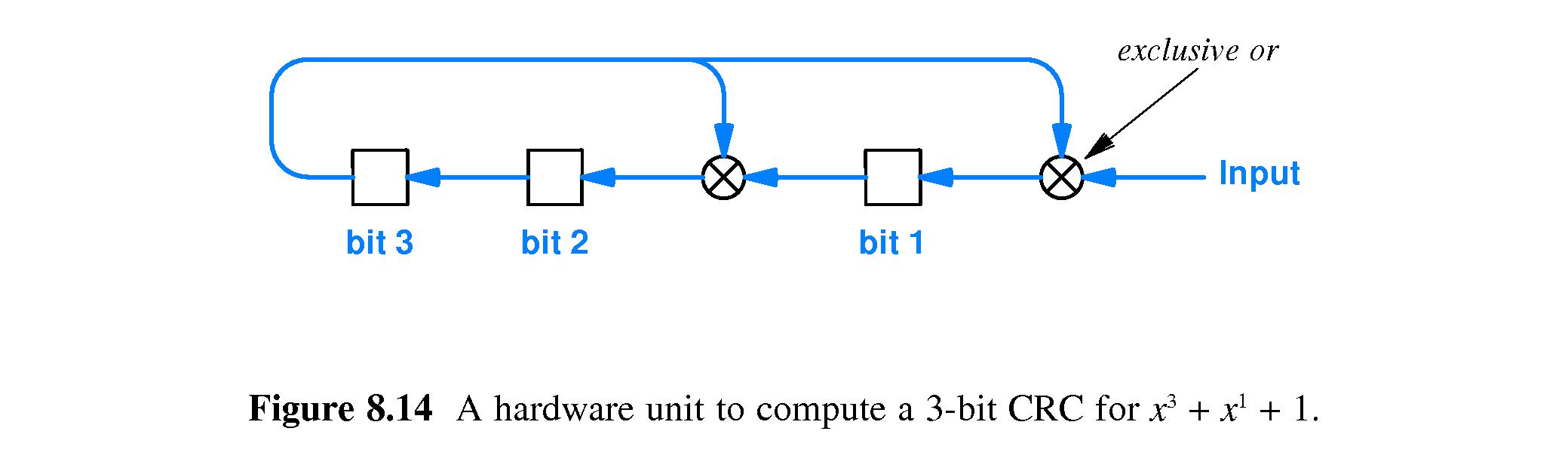
  • CRC hardware can be implemented as a shift register with XOR gates between some of the bits.
  
  
  
  
• 8.15 Automatic Repeat reQuest (ARQ) Mechanism
  
  
  • The idea of ARQ is for the receiver to acknowledge (only) received messages that appear to be correct.
  • If the sender does not get an acknowledgement of a message after a certain time limit, it retransmits the message.