(rev. 2021/02/13)
Lemma for Verifying MST Algorithms
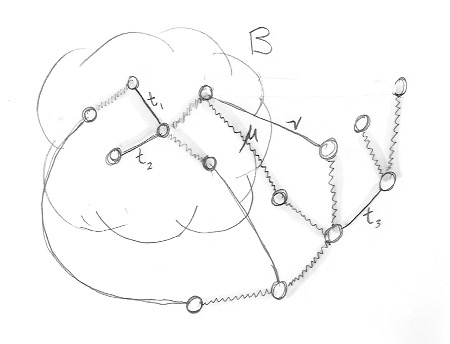 Lemma 6.3.1: Let G=<N, E> be a connected, undirected graph for which a
positive length of each edge is given. Let B ⊂ N be a non-empty subset of N,
such that B is not equal to all of N. Let T ⊂ E be a promising set of edges such that no edge in T leaves B.
Let ν be a shortest edge that leaves B. Then T ∪ {ν} is promising.
Lemma 6.3.1: Let G=<N, E> be a connected, undirected graph for which a
positive length of each edge is given. Let B ⊂ N be a non-empty subset of N,
such that B is not equal to all of N. Let T ⊂ E be a promising set of edges such that no edge in T leaves B.
Let ν be a shortest edge that leaves B. Then T ∪ {ν} is promising.
Proof: T is promising. By definition, that means T ⊂ M,
where M is the edge set of a min cost spanning tree, L = <N, M>,
of G.
Case 1: Suppose ν ∈ M. Then T ∪ {ν} ⊂ M, and so T ∪ {ν}
is promising.
Case 2: Suppose ν ∉ M. Let n be the number of nodes in G.
Then M' = M ∪ {ν} is a set of n edges of G,
and so the graph L' = <N, M'> has a simple cycle C. (A simple cycle
does not cross itself in the middle.)
There's no cycle using just the
edges in M, so ν must be on the cycle C.
The edge ν leaves B, so it
has the form ν = {x,y}, where x ∈ B and y ∉ B. Without loss of generality, we can assume that the cycle C starts by following ν from x to y, and eventually returning to x. Therefore, C eventually returns to B. Therefore there must be another edge, μ, on C such that μ leaves B.
Therefore, if we take the set of edges M'' = (M' - {μ}) = (M ∪ {ν} - {μ}) , and consider the
graph L'' = <N, M''>, L'' is connected and has n-1 edges. Therefore L'' is
a spanning tree of G.
The cost of L'' is no more than the cost of L, because the cost of ν
is no more than the cost of μ. Both ν and μ are edges that leave B,
and ν is a cheapest such edge.
Therefore L'' = <N, M''> is a min cost spanning tree of G.
If t ∈ T, then t ∈ M, because T ⊂ M. Also t ≠ μ, because
μ leaves B, and no edge in T leaves B. Therefore, if t ∈ T, then
t ∈ M - {μ}. This shows that T ⊂ M - {μ}.
It follows that T ∪ {ν} ⊂ M ∪ {ν} - {μ} = M'', and so T ∪ {ν}
is promising.
QED
 Lemma 6.3.1: Let G=<N, E> be a connected, undirected graph for which a
positive length of each edge is given. Let B ⊂ N be a non-empty subset of N,
such that B is not equal to all of N. Let T ⊂ E be a promising set of edges such that no edge in T leaves B.
Let ν be a shortest edge that leaves B. Then T ∪ {ν} is promising.
Lemma 6.3.1: Let G=<N, E> be a connected, undirected graph for which a
positive length of each edge is given. Let B ⊂ N be a non-empty subset of N,
such that B is not equal to all of N. Let T ⊂ E be a promising set of edges such that no edge in T leaves B.
Let ν be a shortest edge that leaves B. Then T ∪ {ν} is promising.