(rev. 2020/02/26)
[2020/02/26: Corrections to definitions of path and cycle]
[2019/01/16: Initial version]

Tree and Graph Properties

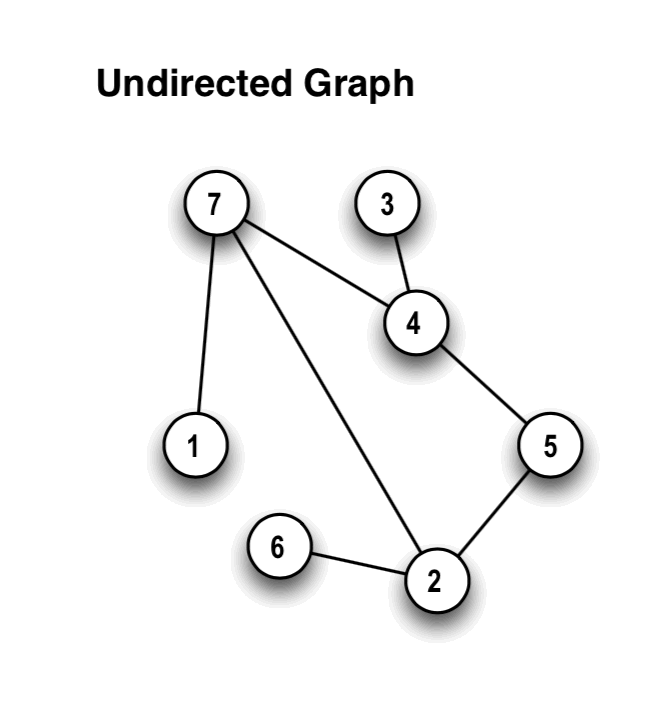sample undirected graph DEFINITION 1: An undirected graph G=<N,E> is a pair of sets. N is a set of nodes. E is the edge set. Each element of E is of the form {μ, ν} where μ∈N, ν∈N, and μ ≠ ν.

(Notice that, unlike the edges of a directed graph, the edges of an undirected graph are sets, not ordered pairs.)

DEFINITION 2: If G=<N,E> is an undirected graph, a path in G is a sequence of nodes
μ1, μ2, ..., μk-1, μk having the property that {μi, μi+1} is an edge, for each consecutive pair of nodes, μi+1 in the sequence. A path is simple if all the nodes in the sequence are distinct from one another. (In other words, a simple path does not cross itself.)

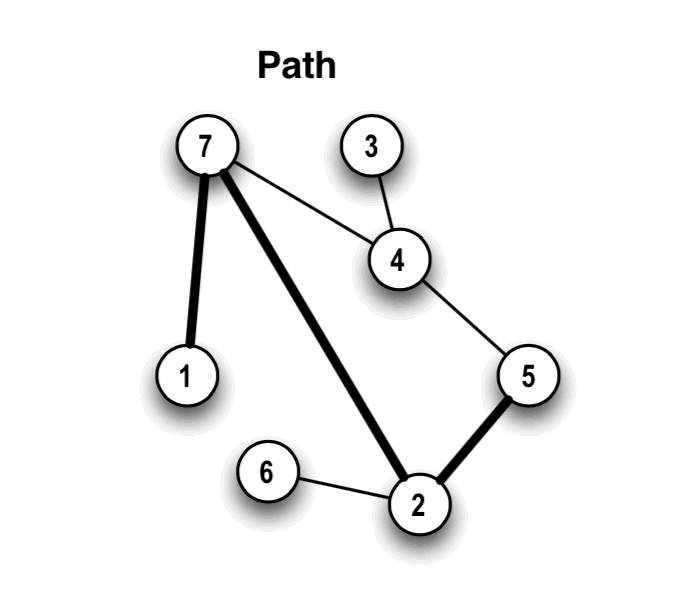sample path in an undirected graph In the figure on the left, 1, 7, 2, 5 is a path. We think of it as a path between 1 and 5. The sequence 3,4 is also a path between 3 and 4. (For technical reasons, sometimes we refer to a single node like 6 as an empty path. So 6 would be considered an empty path from 6 to itself, having no edges.)

Some paths are cycles. A (simple) cycle is a path in which the number of nodes is 3 or more, and in which all the nodes are distinct, except that the last node is equal to the first node.

In the figure on the left, 7, 2, 5, 4, 7 is a cycle. We think of it as a path that returns to its starting point.

DEFINITION 3: An undirected graph G is connected if, for each distinct pair of nodes μ≠ν of G, there is a path between μ and ν.

DEFINITION 4: A tree is an undirected graph T=<N,E> in which there is exactly one path between each distinct pair of nodes.

DEFINITION 5: An undirected graph J=<M,D> is a subgraph of an undirected graph G=<N,E> if
  1. the node set M of J is a subset of the node set, N, of G;
  2. the edge set D of J is a subset of the edge set E of G; and
  3. every edge in D joins two nodes in M.
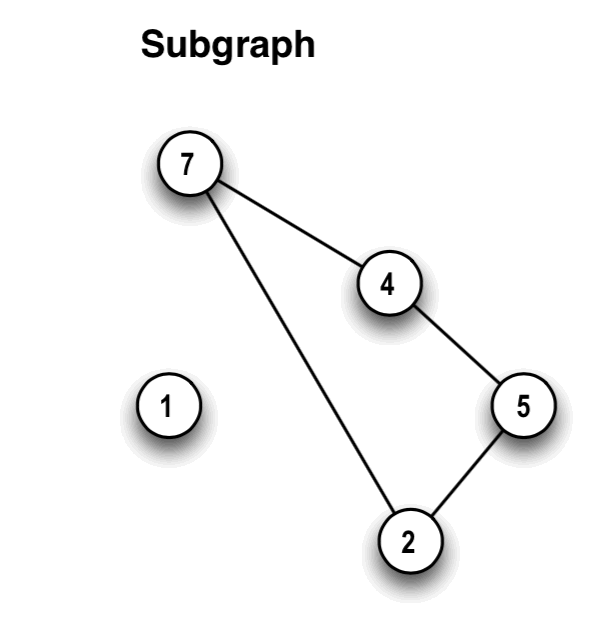example of a subgraph (Less formally stated, we get a subgraph of G by taking some of its nodes, plus some of the edges that join pairs of those nodes.)

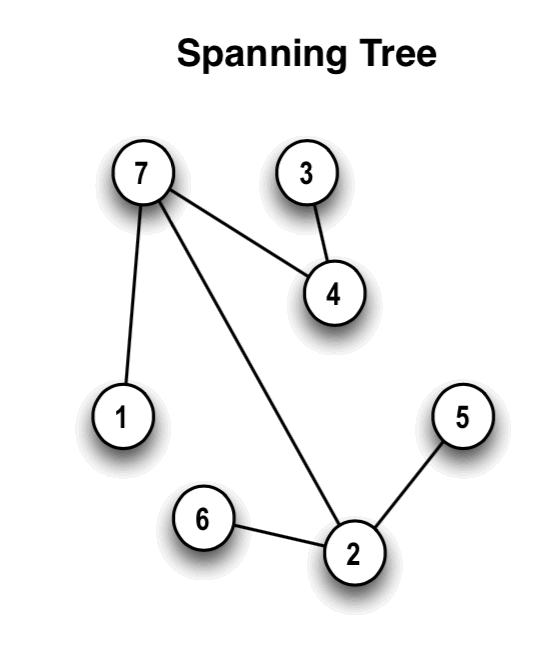
DEFINITION 6: A spanning tree T=<M,D> of a connected, undirected graph G=<N,E> is a subgraph of G such that T is a tree and M=N.

example of a spanning tree PROPOSITION 1: An undirected graph G=<N,E> is a tree if and only if G is connected and contains no cycles.

PROOF: We first prove that if G is a tree, then it is connected and contains no cycles. Well, if G is a tree, then by definition 4, G has a path between each distinct pair of nodes, so it is connected. Can G have a cycle? If a cycle goes through any two nodes μ and ν, then the two "sides" of the cycle are two different paths between μ and ν. So, no, if G is a tree it has no cycles.

To complete the proof, we must show that if G is connected and contains no cycles, then it is a tree. The fact that G is connected tells us that there is at least one path between any two nodes. Is it possible there could be more than one? If there are two paths between x and y, then we get a cycle by traveling from x to y on one of the paths, and from y to x on the other path. Since G has no cycles, G also has only one path between each pair of nodes. Therefore G is a tree, by the definition of a tree.