[rev March 11, 2019]

Achieving Both Fast Finds and Fast Merges with Disjoint Set Structures

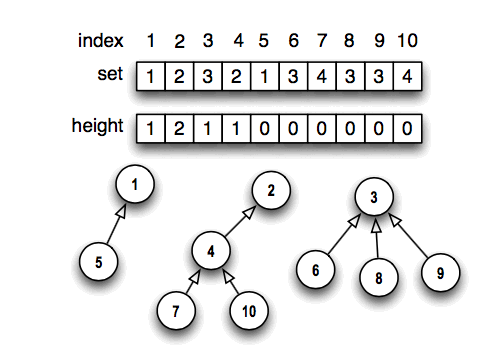representing disjoint sets: version 3 The theorem tells us how to keep the tree heights O(log(N)) if we monitor the height of the trees. Accordingly we work with two arrays. Set is the same as in the previous implementation, and height[i] denotes the (edge) height of the tree rooted at node i.

We begin by initializing all the entries of set as set[i]=i, and all the entries of height as height[i]=0. The operations are defined as follows. 
int Find2.5 (int x) 
{
       /* same as Find2 */
    int r=x ;
    while (set[r] != r) r = set[r] ;
    return r ;
}
void Merge3(int s, int t) 
{
    if (height[s] == height[t])
    {
        height[s]++ ;
        set[t] = s ;
    }
    else 
    {
        if   ( height[s] > height[t] ) 
             set[t] = s ;
        else set[s] = t ;
    }
}
In the worst case, Merge3 is Θ(1) work, and using Merge3 ensures that Find2.5 (same as Find2) does Θ(log(N)) work. Thus doing M finds and N-1 merges involves O(N+Mlog(N)) work.

We can improve Find2.5. The trick is to add "path compression" to Find2.5.

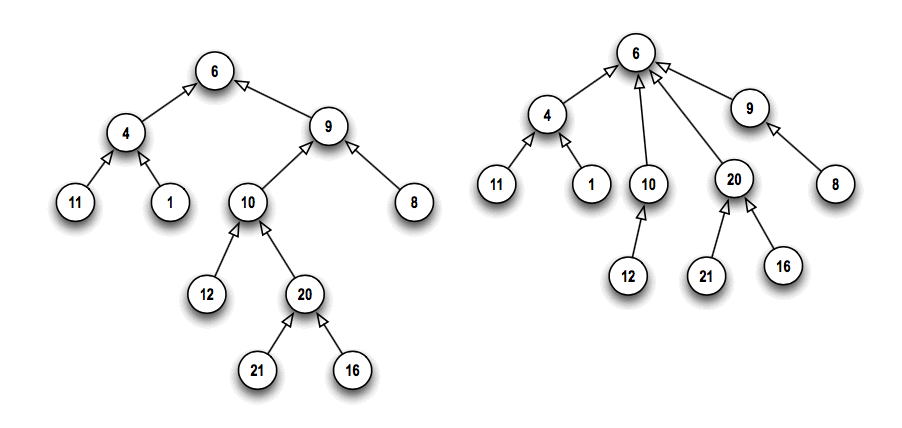
sample tree before and after path compression

Above on the right, you see the effect of starting with the graph on the left, and doing a Find(20) operation, along with path compression. After we find the root, 6, we take the subtrees rooted at 20 and 10, and attach them directly to node 6.

Such path compression could be a worthwhile modification if there's a need to do a great many find operations. The new version of find, Find3, will have average performance extremely close to O(1). Therefore the total work for M finds and N-1 merges will be very close to O(M+N).

Here is pseudo-code for the new Find: 
int Find3 (int x) 
{
    int r=x ;
        /* Find the root r. */
    while (set[r] != r) r = set[r] ; 
    int j, i=x ; /* Start back at x. */
    while (i != r)
    {
        j = set[i] ; /* Save parent of i. */
           /* Connect tree rooted at i directly 
              to the overall root of the tree. */
        set[i] = r ; 
           /* Resume the climb from the position 
              of the old parent. */
        i = j ;
    }
    return r ;
}
Notice that, in Find3, the statement { set[i] = r ; } may reduce the height of various subtrees of the tree rooted at r (by cutting out one of its subtrees). Yet, the code of Find3 does not update the value in the height array corresponding to any of those subtrees. So in cases where we use Find3 and Merge3, we know only that height[ν] is an upper bound on the height of the tree rooted at ν. However, by using these upper bounds in Merge3, we are still assured that the height of of a tree with k nodes is no more than log(k). Therefore, everything we concluded about big-O and big-Θ performance from that theorem remains valid.