The "Log Height" Theorem for Trees Representing Disjoint Sets

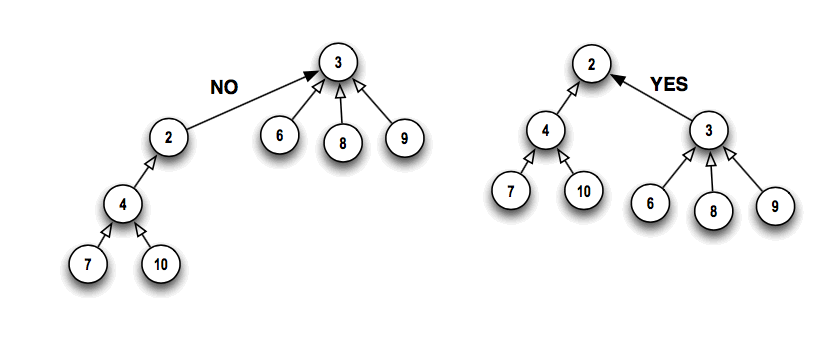
• When merging, what if we insist on making the lower height tree the subtree of the greater height tree? Then if the two heights h₁ and h₂ are not equal, the height of the new tree will be max{h₁, h₂}, else the new height will be h₁ + 1.
  
  
• The figure above is an example. On the right, the new tree is no higher than the taller of the two subtrees that were joined. On the left, the new tree is higher than both subtrees.
  
  
• Theorem 5.9.1(version b) Using the merging technique described above, after an arbitrary sequence of merge operations starting from the initial situation (N singletons), a tree containing k nodes has (edge) height less than or equal to log(k). (Logs in this discussion are all base-2.)
  
  
• PROOF We proceed by induction on k. If k=1, the edge height is 0, and also log(k)=log(1)=0. So 0=height-of-tree ≤ log(k)=0 is true for a tree with k=1 node. That is our base case.
  
  Suppose now that the theorem is true for all positive integers j, such that 1 ≤ j ≤ k-1, where k>1. Suppose that we proceed with building up trees using the merging technique described, and suppose we get to the point where a tree with k nodes has been formed by merging a tree with y nodes and a tree with z nodes. Assume the variable names y, z were chosen so that y ≤ z. Note the following observations:
  
  
  1. k = y+z.
  2. Neither y nor z is zero, because in the process we defined, the trees that are merged are never empty - they all start out containing a single node, and they can only grow larger.
  3. Both y and z are less than k. This follows from the facts that neither y nor z is 0 and that y+z adds up to k.
  4. y≤k/2 If not, then both y and z would be greater than k/2, which would make their sum, k, greater than (k/2)+(k/2)=k. Obviously k>k is false.
  
  Let h_y, h_z, and h_k be the respective (edge) heights of the three trees.
  
  Case #1: If h_y ≠ h_z, then h_k=maximum{h_y, h_z}. In particular, h_k = h_y or h_k = h_z.
  
  Using the inductive hypothesis, we may assume that h_y ≤ log(y) and h_z ≤ log(z).
  
  Therefore, one or the other of the following statements is true
  1. h_k = h_y ≤ log(y) ≤ maximum{log(y), log(z)}
  2. h_k = h_z ≤ log(z) ≤ maximum{log(y), log(z)}
  
  In either case, it follows that h_k ≤ maximum{log(y), log(z)}.
  
  Also, because log is an increasing function, and because y<k, and z<k, maximum{log(y), log(z)} < log(k). Therefore, if h_y ≠ h_z, h_k ≤ log(k).
  
  Case #2: If h_y = h_z, then h_k = 1 + h_y ≤ 1 + log(y). Since y≤k/2, 1 + log(y) ≤ 1 + log(k/2) = 1 + log(k) - 1 = log(k). It follows from this that h_k ≤ log(k).
  
  We've proved the inductive step for all cases, so this completes the proof.