[Latest version: Feb 14, 2021]

Disjoint Set Structures (the union-find problem)

N objects, each initially contained in a singleton set. At any time the N objects are grouped into a collection of sets, each of which is disjoint from the others. Empty sets do not occur. One element of each set is designated to be the label of the set. We are interested in two operations on such collections:

Find(u) returns the label of the set containing u.

Merge(s, t) merges the two sets with labels s and t into one set. (Assume s ≠ t)

This defines a data structure with two operations. It is important to find efficient implementations, because that provides a way to eliminate bottlenecks from several algorithms.

DISCUSSION

First Implementation

By using a suitable mapping, we may assume that the N objects are just the integers from 1 to N.
Suppose that the smallest element of a set is always chosen to be the label.
To represent the collection of sets we can use a single array called "set."

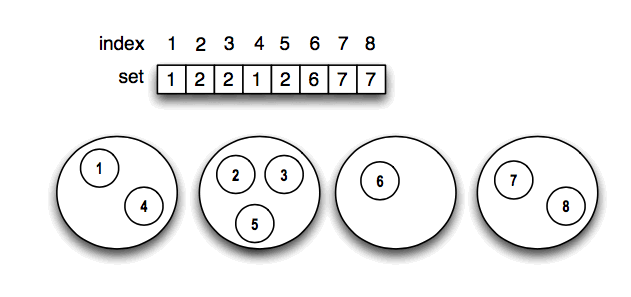
sample representation of disjoint sets: version 1

Here, set[i] is the label of the set containing i. With this representation, we can implement the operations as follows:

int Find1(int x) {return set[x] ; }

void Merge1(int s, int t) 
{
    int k;
    if (t < s) swap (s,t) ; 
      /* Now s is the label for the new set. */
      /* Next replace every t in the array with s. */
    for (k=1; k≤N; k++) if (set[k]==t) set[k]=s ;
}

Notes

Find1 does Θ(1) work.
Merge1 does Θ(N) work.
Each invocation of Merge1 reduces the number of sets by one. Therefore, after N-1 merges, there will be exactly one set containing all the elements.
In this implementation, it requires Θ(N²) work to execute N-1 merges.

Second Implementation

Use the array, set, to represent each individual set as a 'tree.'

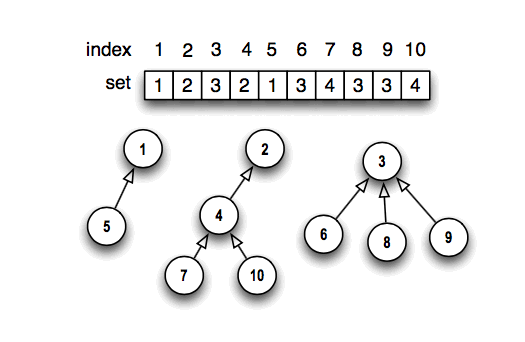
sample representation of disjoint sets: version 2

Now set[i] = the 'parent' of element i in the set-tree containing i. (Roots are considered their own parent.) The array above represents the forest of trees shown below it, which in turn represents the sets {1,5}, {2,4,7,10}, and {3,6,8,9}.

With this representation, we can implement the operations as follows:

int Find2(int x) 
{  
    int r=x ;
       /* Climb from x to the root. */
    while (set[r] != r) r=set[r] ;
    return r ;
}

void Merge2(int s, int t) 
{
    if   (s < t) set[t] = s ; /* s is the label */
    else set[s] = t ;         /* t is the label */
}

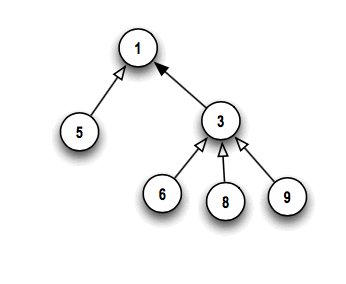
The example above illustrates that we can do a merge by pointing the root with the larger value at the root with the smaller value.

Notes

It is important to understand that this tree structure we have introduced has nothing to do with any relationships that may already exist among the objects in the sets. Trees that represent sets are only structures that we impose in order to get more efficient find and merge operations. In particular, if we use the structure to help find a spanning tree of a graph, any resemblance between the structure of the spanning tree and the structure of the trees representing the disjoint sets is merely coincidental.
Find2 does Θ(log(N)) work, if the tree is "bushy" (O(log(n) height)).
Merge2 does Θ(1) work.
If we do O(N) finds and merges, which is typical, the amount of work will be O(Nlog(N)), assuming the trees are bushy.