Latest version: Feb 08, 2021

Thinking about how to Improve the Efficiency of the Adjacency-Matrix Version of Dijkstra's Algorithm

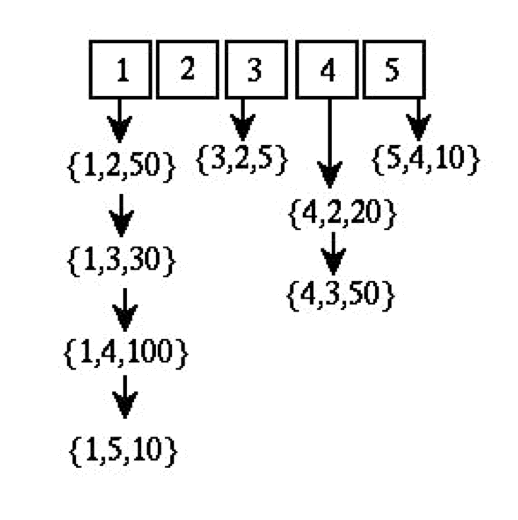
Note: in the inner for-loop of the 'adjacency-matrix' version of Dijkstra's Algorithm, it would suffice to examine only nodes ω ∈ C such that there is an edge ν--> ω. If we use an array of edge lists (as in the figure) to represent the graph G, instead of an adjacency-matrix, then we could save time checking to see for which nodes ω ∈ C there is an edge ν-->ω.

If we use the adjacency-matrix, we have to check each entry of the form (ν, ω) for each ω ∈ C to see if the edge exists. On average the number of elements in C is about n/2, which means this part of the algorithm will be Θ(n²) overall.

If we use the edge list structure instead of the adjacency-matrix, we can just scan down the edge list of ν and find all edges leaving ν, without any failed tests. There is, it is true, the disadvantage that some of the edges we find on the list may go to nodes that are not in C. An edge may go to a node in S. Nonetheless, using this method, each edge e=(x,y) of G will be processed at most once, in the run through the greedy loop body that happens when x is added to S.

Consequently, if m << n², then that part of the algorithm would be Θ(m): a savings over Θ(n²).

However, this instruction

ν = some element of C with smallest value of Dist[ν] ;

would still make the algorithm Θ(n²) overall unless we find a way to do it more efficiently. We could select each ν in Θ(log(n)) time if the nodes were organized in a priority queue implemented as a heap. (Low value of Dist[ν], would mean ν has high priority. We'd have to delete the top element of the heap each time we add a node to S, and that deletion would be a Θ(log(n)) operation.)

If the algorithm used such a priority queue, it might have to promote (sift up) an element ω in the heap after decreasing the value of Dist[ω] in the inner for-loop of the pseudo-code. However it could do that in Θ(log(n)) time.

Overall that would mean doing Θ(log(n)) work n-2 times to choose n-2 values of ν for insertion into S, plus doing Θ(log(n)) work at most m times to update the Dist values of nodes in the priority queue.

Thus the total work would be Θ((n+m)*log(n)). If the graph is connected, this can be simplified to Θ((m)*log(n)).

Proof: In that case, the number of edges m is at least n-1, so m ≥ n/2 and n ≤ 2m (for n > 1). From that we can conclude that m < m+n ≤ m + 2m when n > 1, which shows that m+n is Θ(m), and therefore that Θ(m) and Θ(m+n) are the same when the graph is connected.

We can assume that the graph has been selected in advance to be connected, because there is no point in searching for shortest paths where there are no paths. (It does not require too much work. Chapter 3 of "Algorithm Design" by Kleinberg/Tardos discusses the fact that we can find the connected components of a directed graph with O(m+n) work, where m and n are the numbers of edges and nodes in the connected component.)

So the conclusion is that, given a connected directed graph with m << n², there is a Θ(m*log(n)) version of Dijkstra's Algorithm that can be significantly more efficient than the 'naive' adjacency-matrix version we looked at first. If m << n², the ratio n² / m*log(n) converges to ∞ as n--> ∞, so this 'new' algorithm is sure to be worthwhile if the input is a sparse graph that has a large enough number of nodes.

However, if m is Θ(n²) then the naive method will be more efficient (in the big-O sense), because the ratio would become a positive constant times n² / n²*log(n), which is 1/log(n), which converges to 0 as n--> ∞.

Note: the preceding analysis applies to the worst case. For example, the sift operations are Θ(log(n)) in the worst case.