A Worst-Case Analysis of the Adjacency-Matrix Version
of Dijkstra's Algorithm
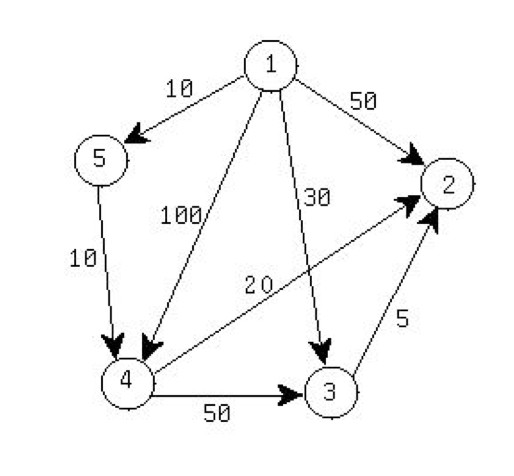
THE PSEUDO-CODE:
/* n = #nodes. Let m = #edges. */
Initialize a set C = {2, 3, ... , n} ;
For i from 1 to n
{
Initialize Dist[i] = EdgeLength[1,i] ;
Initialize BackPoint[i] = 1 ;
}
/* The work above would be initialization
of three arrays of size Θ(n). */
Do n-2 times /* Θ(n) repetitions of the loop body */
{
/* find item in list of average Θ(n) size,
Θ(n) work */
ν = some element of C with smallest value of Dist[ν] ;
C = C-{ν} ; /* O(1) work to delete ν */
/* Below we do O(1) work for each of average of Θ(n) items,
Θ(n) work*/
For each ω in C such that there is an edge ν-->ω
{
If Dist[ω] > Dist[ν] + EdgeLength[ν,ω]
Then
{
Dist[ω] = Dist[ν] + EdgeLength[ν,ω] ;
BackPoint[ω] = ν ;
}
}
} /* The loop that ends here does Θ(n) repetitions, and each rep
does Θ(n) work. That's Θ(n2) work overall
for the loop. */
Return Dist and BackPoint as the output ;
/* The work done above is dominated by the loop. So it is a
Θ(n2) algorithm. */

