heaps, heapsort, and priority queues

(Latest Revision: Feb 14, 2019)
(Prior Revision: 04/05/2004)

Heaps, Heapsort, and Priority Queues

First, a brief review of one of the common means used to represent a binary tree.


This array X:

          A   E   R   I   -   L   -   T   Z   -   -
indices   1   2   3   4   5   6   7   8   9   10  11

represents this tree:       
                 
             A        
            / \       * parent(X[n])  X[floor(n/2)]
           /   \      *  if (n even) 
          /     \             sibling(X[n]) = X[n+1] 
         E       R       else sibling(X[n]) = X[n-1] 
        /       /     * left child(X[n]) = X[2n]
       /       /      * right child(X[n]) = X[2n+1]
      /       /
     I       L
    / \ 
   /   \ 
  T     Z

Advantages:
- compact representation of 'complete' trees
- no explicit pointers, yet 'implicit' pointers are easy to follow
- several kinds of implicit pointers: child, parent, and sibling
Disadvantages:
- not a compact representation for binary trees of some shapes
- storage is not dynamic (fixed array size limitation)

Definition: A heap is a complete binary tree whose nodes contain search keys that are arranged in order all along every path from the root to any leaf.

The array representation of a binary tree described above, at the beginning of this document, can represent heaps compactly - without wasting memory.

The keys of a heap are elements of a totally ordered set - laws of trichotomy and transitivity hold true.

If the order chosen for the heap keys is descending then the heap is called a max heap. In a max heap, the largest key in the tree is always in the root node. On the other hand, if the order chosen for the heap keys is ascending then the heap is called a min heap. In a min heap, the smallest key is always in the root node.

Here are three examples of min heaps.

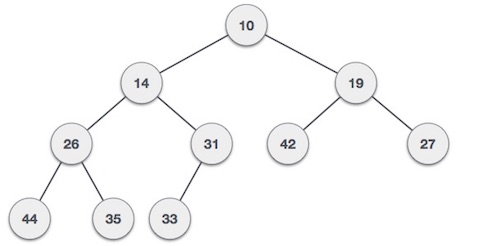
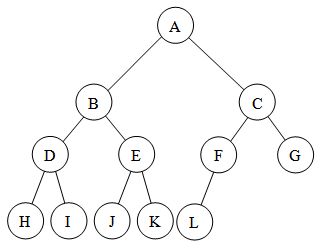
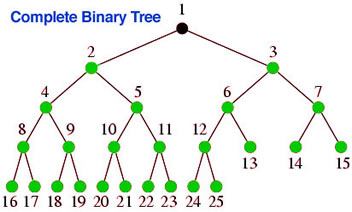
Although the examples we gave above were min heaps, the rest of the discussion below uses max heaps as examples.

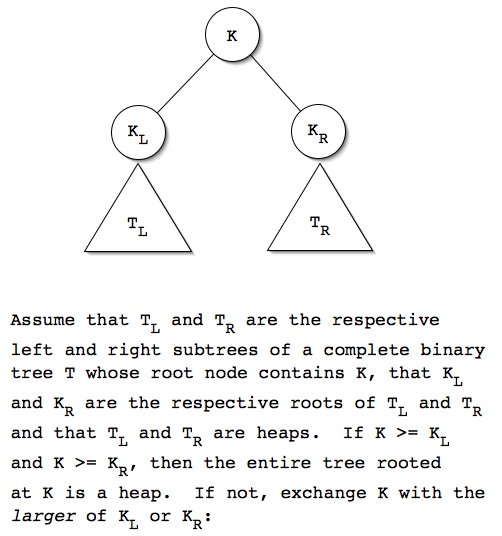
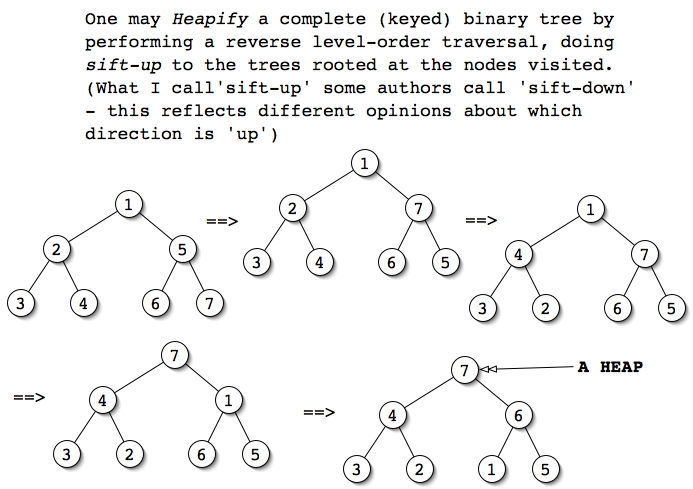
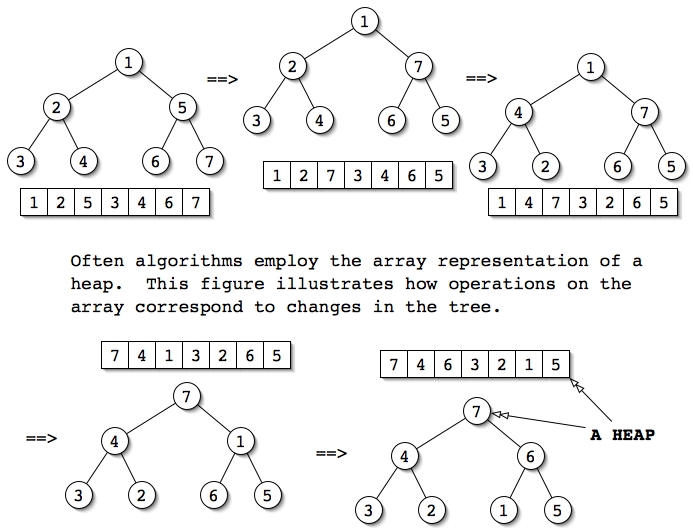
Theorem: Heapification is Θ(N) where N equals the number of nodes in the complete keyed binary tree.

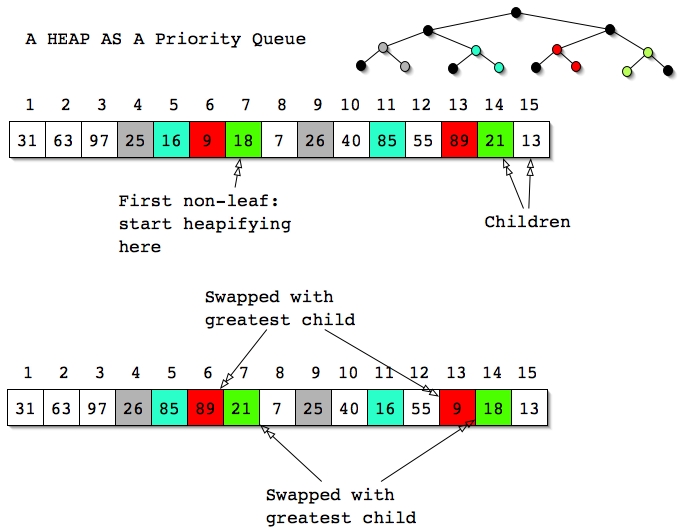
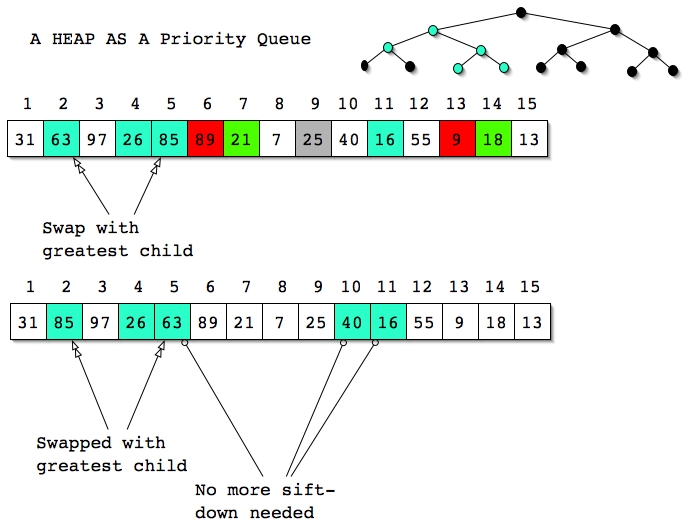
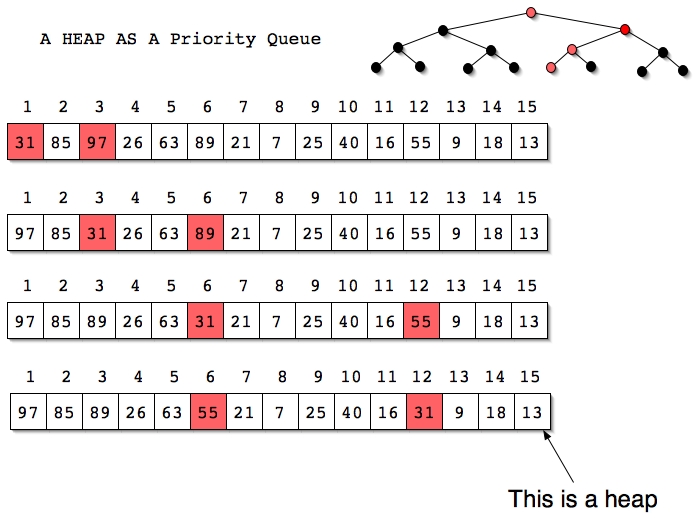
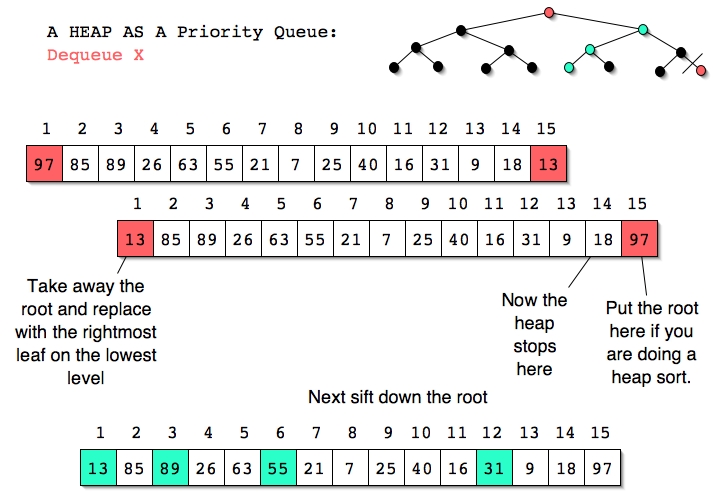
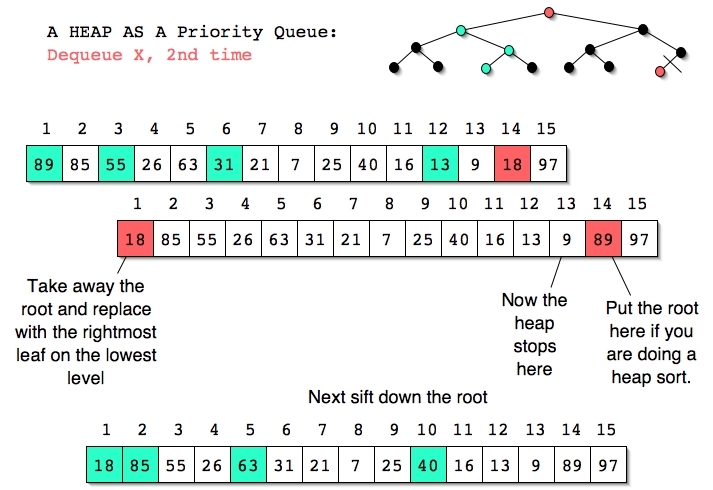
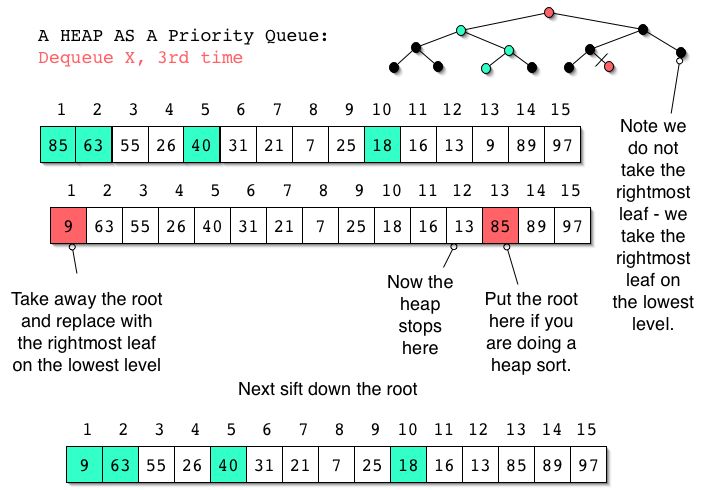
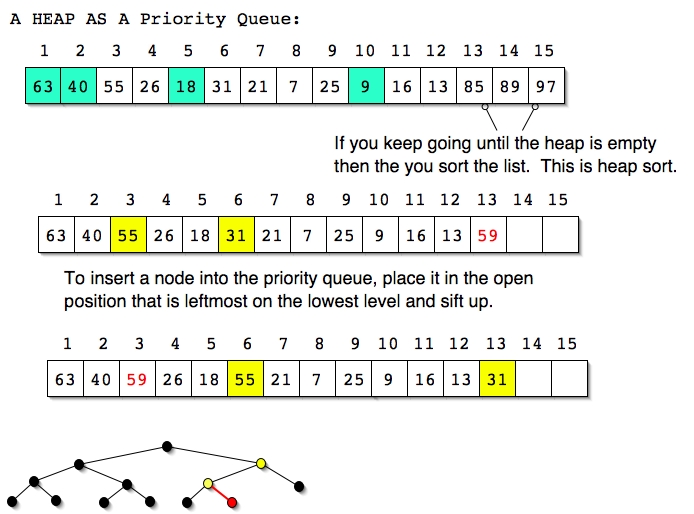
We can see from the examples and accompanying description that Dequeue and Enqueue are O(logN) operations in a priority queue implemented with a heap as described.

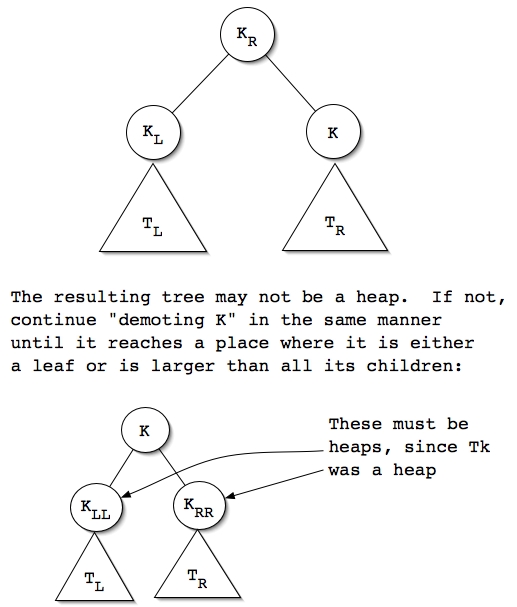
In some algorithms that use the priority queue, we want an operation that changes the priority of an element of the queue - "changePriority". When we change the priority of an item, it may 'destroy' the order property of the heap. However we can restore that order just by either sifting the item up or down along some path between the root and a leaf. That work is O(logN) too.

In applications that use the changePriority operation, usually the data structure includes an external index that keeps track of the positions of all the items in the priority queue. In other words, the index keeps track of where the items are in the array that is the implementation of the heap. We can create the index in linear time and it only requires constant time to update it each time an item is moved to a different position in the heap. Because we have the index, we can find any item in the heap in constant time. We don't have to search for it. So if we are just given the 'name' of an item and told to change its priority, we can find it, change the priority, and restore the heap order property in O(logN) time.